��Ŀ����
����Ŀ����ͼ��һ�κ���y��kx��4��k��0����ͼ����y�ύ�ڵ�A���뷴��������y��![]() ��x��0����ͼ���ڵ�B��6��b����
��x��0����ͼ���ڵ�B��6��b����
��1��b��__________��k��__________��
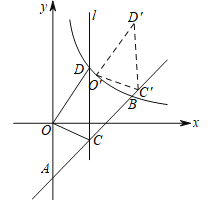
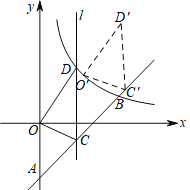
��2����C��ֱ��AB�ϵĶ��㣨���A��B���غϣ�������C��ƽ����y���ֱ��l�����������������ͼ���ڵ�D������C�ĺ�����Ϊ3ʱ������OCD���ֽ���OCD������AB����ƽ��һ���ľ��루��ͼ�����õ���O��C��D��������O�Ķ�Ӧ��O�����ڸ÷���������ͼ���ϣ����O����D�������꣮
���𰸡� ��1��2�� 1����2��![]() ,
, ![]() .
.
�������������������1����B��6��b������![]() ���ɵ�b��ֵ���ѵ�B���������һ�κ�������ʽ�����ɵõ�k��ֵ��
���ɵ�b��ֵ���ѵ�B���������һ�κ�������ʽ�����ɵõ�k��ֵ��
��2���ȸ��ݵ�C�ĺ�����Ϊ3����õ�C��D�����꣬��O'��a�� ![]() ������C'��a+3��
������C'��a+3�� ![]() ��1�������ݵ�C'��ֱ��y=x��4�ϣ��ɵ÷���
��1�������ݵ�C'��ֱ��y=x��4�ϣ��ɵ÷���![]() ��1=a+3��4�������õ�a��ֵ�������ó���O����D�������꣮
��1=a+3��4�������õ�a��ֵ�������ó���O����D�������꣮
����������⣺��1������B�ڷ���������![]() ��x��0����ͼ���ϣ���B��6��b������
��x��0����ͼ���ϣ���B��6��b������![]() ����b=2����B��6��2��������B��ֱ��y=kx��4�ϣ���2=6k��4�����k��1���ʴ�Ϊ��2��1��
����b=2����B��6��2��������B��ֱ��y=kx��4�ϣ���2=6k��4�����k��1���ʴ�Ϊ��2��1��
��2������C�ĺ�����Ϊ3����x=3����y=x��4����y=��1����C��3����1������CD��y�ᣬ����D�ĺ�����Ϊ3����x=3����![]() ���ɵ�y=4����D��3��4����
���ɵ�y=4����D��3��4����
��ƽ�ƿɵã���OCD�ա�O'C'D'����O'��a�� ![]() ������C'��a+3��
������C'��a+3�� ![]() ��1��������C'��ֱ��y=x��4�ϣ���
��1��������C'��ֱ��y=x��4�ϣ���![]() ��1=a+3��4����
��1=a+3��4����![]() =a����a��0����a=
=a����a��0����a=![]() ����O'��
����O'��![]() ��
�� ![]() ������D'��
������D'��![]() +3��
+3�� ![]() +4����
+4����