Question

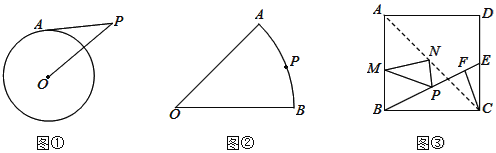
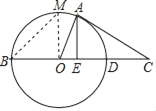
【题目】如图，PA、PB是半径为1的⊙O的两条切线，点A、B分别为切点，∠APB＝60°，OP与弦AB交于点C，与⊙O交于点D．阴影部分的面积是_____（结果保留π）．

Answer 1

【答案】.

【解析】

由PA、PB是半径为1的⊙O的两条切线，得到OA⊥PA，OB⊥PB，OP平分∠APB，而∠APB=60°，得∠APO=30°，∠POA=90°﹣30°=60°，而OP垂直平分AB，得到S△AOC=S△BOC，从而得到S阴影部分=S扇形OAD，然后根据扇形的面积公式计算即可．

∵PA、PB是半径为1的⊙O的两条切线，∴OA⊥PA，OB⊥PB，OP平分∠APB，而∠APB=60°，∴∠APO=30°，∠POA=90°﹣30°=60°．

又∵OP垂直平分AB，∴△AOC≌△BOC，∴S△AOC=S△BOC，∴S阴影部分=S扇形OAD．

故答案为：．