题目内容
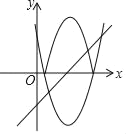
【题目】课堂上，老师给出一道题：如图，将抛物线C：y＝x2﹣6x+5在x轴下方的图象沿x轴翻折，翻折后得到的图象与抛物线C在x轴上方的图象记为G，已知直线l：y＝x+m与图象G有两个公共点，求m的取值范围甲同学的结果是﹣5＜m＜﹣1，乙同学的结果是m＞
．下列说法正确的是（ ）
A.甲的结果正确
B.乙的结果正确
C.甲、乙的结果合在一起才正确
D.甲、乙的结果合在一起也不正确
【答案】D
【解析】
当直线过抛物线与x轴右侧的交点时，恰有一个交点；
直线y＝x+m向上移，经过g左侧交点之前均为两个交点；
继续向上平移，直到经过G中间的顶点（3，4）之前均为三个交点；
最终向上平移，均有两个交点.
解：令y＝x2﹣6x+5＝0，解得（1，0），（5，0）
将点（1，0），（5，0）分别代入直线y＝x+m，得m＝﹣1，﹣5；
∴﹣5＜m＜﹣1
由题可知，图象G中的顶点为（3，4）
代入直线y＝x+m，得m＝1，
∴m＞1
综上所述，m＞1或﹣5＜m＜﹣1
故选：D．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
