Question

【题目】如图，二次函数y＝﹣（x﹣2）2+b的图象与x轴分别相交于A、B两点，点A的坐标为（﹣1，0），与y轴交于点C．

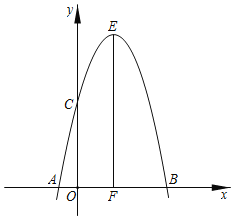
（1）求b的值；

（2）抛物线顶点为E，EF⊥x轴于F点，点P（2，m）是线段EF上一动点，Q（n，0）在x轴上，且n＜2，若∠QPC＝90°，求n的最小值．

Answer 1

【答案】（1）b=9;（2）

【解析】

（1）将点A的坐标代入二次函数表达式，即可求解；

（2）利用tan∠MCP＝tan∠QPF，则，即可求解．

（1）将点A的坐标代入二次函数表达式得：0＝﹣（﹣1﹣2）2+b，

解得：b＝9；

（2）过点C作CM⊥EF，垂足为M，

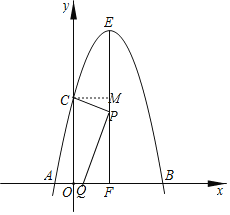
∴∠CMP＝∠CPQ＝∠PFQ＝90°

∴∠MCP＝∠QPF，

∴tan∠MCP＝tan∠QPF，

∴，

∴n＝，

∵n＜2，∴0≤m＜5，

∴当时，n的最小值为﹣．