Question

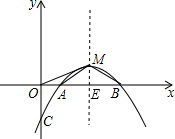
如图，已知抛物线y=ax²+bx+c（a≠0）的顶点M在第一象限，抛物线与x轴相交于A、B两点（点A在点B的左边），与y轴交与点C，O为坐标原点，如果△ABM是直角三角形，AB=2，OM=

5

．
（1）求点M的坐标；
（2）求抛物线y=ax²+bx+c的解析式；
（3）在抛物线的对称轴上是否存在点P，使得△PAC为直角三角形？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．

Answer 1

（1）

∵点M为抛物线的顶点，
∴MA=MB，
又∵△ABM是直角三角形，
∴△AMB是等腰直角三角形，
∵AB=2，
∴ME=1，
在Rt△OME中，可得OE=

OM2-ME2

=2，
故可得点M的坐标为（2，1）．
（2）∵AE=BE=

1

2

AB=1，OE=2，
∴OA=1，OB=3，
∴点A的坐标为（1，0），点B的坐标为（3，0），
将点A、B、M的坐标代入抛物线解析式可得：

a+b+c=0 9a+3b+c=0 4a+2b+c=1

，
解得：

a=-1 b=4 c=-3

，
故抛物线的解析式为：y=-x²+4x-3．
（3）设点P的坐标为（2，y），
则AC²=10，AP²=1+y²，CP²=4+（y+3）²，
①当∠PAC=90°时，AC²+AP²=CP²，即10+1+y²=4+（y+3）²，
解得：y=-

1

3

，
即此时点P的坐标为（2，-

1

3

）；
②当∠PCA=90°时，AC²+CP²=AP²，即10+4+（y+3）²=1+y²，
解得：y=-

11

3

，
即此时点P的坐标为（2，-

11

3

）；
③当∠APC=90°时，AP²+CP²=AC²，即1+y²+4+（y+3）²=10，
解得：y=-1或-2，
即此时点P的坐标为（2，-1）或（2，-2）；
综上可得点P的坐标为（2，-

1

3

）或（2，-

11

3

）或（2，-1）或（2，-2）．