题目内容
已知如图,抛物线t=ax2+bx+c与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交 于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴负半轴上的一个动点,直线MB交抛物线于N,交⊙P于D.
于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴负半轴上的一个动点,直线MB交抛物线于N,交⊙P于D.
(1)填空:A点坐标是______,⊙P半径的长是______,a=______,b=______,c=______;
(2)若S△BNC:S△AOB=15:2,求N点的坐标;
(3)若△AOB与以A、B、D为顶点的三角形相似,求MB•MD的值.
 于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴负半轴上的一个动点,直线MB交抛物线于N,交⊙P于D.
于A点,过A、B、C三点的⊙P与y轴相切于点A,M为y轴负半轴上的一个动点,直线MB交抛物线于N,交⊙P于D.(1)填空:A点坐标是______,⊙P半径的长是______,a=______,b=______,c=______;
(2)若S△BNC:S△AOB=15:2,求N点的坐标;
(3)若△AOB与以A、B、D为顶点的三角形相似,求MB•MD的值.
(1)将B(1,0)、C(4,0)两点坐标代入抛物线t=ax2+bx+c得:
解得
①
由题意可知:PA=PB=PC,且PA⊥y轴,
设P点坐标为P(2.5,yA ),由题意可知PA=PB=PC=2.5,
根据勾股定理可求得yA=2,
∴A点坐标是(0,2),⊙P半径为的长为2.5,
将A点坐标代入抛物线方程可得2=c,
联立①式便可解得a=0.5,b=-2.5,c=2.
∴抛物线的方程为t=0.5x2-2.5x+2,
故答案为:(0,2),2.5,0.5,-2.5,2;
(2)S△BNC:S△AOB=
=
=
,
解得yN=5,
将yN=5代入抛物线的方程t=0.5x2-2.5x+2得:x1=-1,x2=6,
观察图形可知x2=6符合题意,
∴N点的坐标为N(6,5);
(3)由题意可知△AOB∽△DBA,
=
=
,
∵OA=2,OB=1,
由勾股定理可知AB=
,根据三角形相似可知BD=2
,
由射影定理可知:AB2=MB×BD,
(
)2=MB×2
,
解得MB=
,MD=MB+BD=
,
∴MB•MD=
×
=
.
|
解得
|
由题意可知:PA=PB=PC,且PA⊥y轴,
设P点坐标为P(2.5,yA ),由题意可知PA=PB=PC=2.5,
根据勾股定理可求得yA=2,
∴A点坐标是(0,2),⊙P半径为的长为2.5,
将A点坐标代入抛物线方程可得2=c,
联立①式便可解得a=0.5,b=-2.5,c=2.
∴抛物线的方程为t=0.5x2-2.5x+2,
故答案为:(0,2),2.5,0.5,-2.5,2;
(2)S△BNC:S△AOB=
| ||
|
| 3×yN |
| 1×2 |
| 15 |
| 2 |
解得yN=5,
将yN=5代入抛物线的方程t=0.5x2-2.5x+2得:x1=-1,x2=6,
观察图形可知x2=6符合题意,
∴N点的坐标为N(6,5);
(3)由题意可知△AOB∽△DBA,
| AB |
| DA |
| AO |
| DB |
| OB |
| BA |
∵OA=2,OB=1,
由勾股定理可知AB=
| 5 |
| 5 |
由射影定理可知:AB2=MB×BD,
(
| 5 |
| 5 |
解得MB=
| ||
| 2 |
5
| ||
| 2 |
∴MB•MD=
| ||
| 2 |
5
| ||
| 2 |
| 25 |
| 4 |

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目



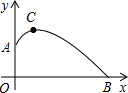
 点P的坐标(t,T)满足的关系,若不存在说明理由.
点P的坐标(t,T)满足的关系,若不存在说明理由.