题目内容
【题目】直线y=kx+3和x轴、y轴的交点分别为B、C,∠OBC=30°,点A的坐标是(![]() ,0),另一条直线经过点A、C.
,0),另一条直线经过点A、C.
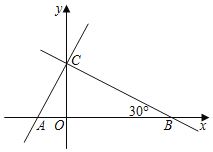
(1)求点B的坐标及k的值;
(2)求证:AC⊥BC;
(3)点M为直线BC上一点(与点B不重合),设点M的横坐标为x,△ABM的面积为S.
①求S与x的函数关系式;
②当S=6![]() 时,求点M的坐标.
时,求点M的坐标.
【答案】(1)B(3![]() ,0),k=﹣
,0),k=﹣![]() ;(2)见解析;(3)①S=
;(2)见解析;(3)①S=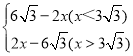 ;②点M的坐标为(0,3)或(6
;②点M的坐标为(0,3)或(6![]() ,-3).
,-3).
【解析】
(1)直线y=kx+3和y轴的交点为C,则点C(0,3),则BC=6,OB=3![]() ,则点B(3
,则点B(3![]() ,0),即可求解;
,0),即可求解;
(2)OA=![]() ,OC=3,则AC=2
,OC=3,则AC=2![]() ,则∠ACO=30°,即可求解;
,则∠ACO=30°,即可求解;
(3)①点M(x,-![]() x+3),S=
x+3),S=![]() ×AB×|yM|即可求解;
×AB×|yM|即可求解;
②将S=6代入①中的函数关系式,即可求解.
解:(1)直线y=kx+3和y轴的交点为C,则点C(0,3),
则BC=6,OB=3![]() ,
,
则点B(3![]() ,0),
,0),
将点B的坐标代入y=kx+3得:0=3![]() k+3,
k+3,
解得:k= -![]() ;
;
(2)在Rt△AOC中,OA=![]() ,OC=3,由勾股定理得AC=2
,OC=3,由勾股定理得AC=2![]() ,
,
∴∠ACO=30°,
∵∠OBC=30°,
∴∠BCO=60°,
∴∠ACB=∠ACO+∠BCO=90°,
∴AC⊥BC;
(3)①直线BC的表达式为:y=﹣![]() x+3,则点M(x,﹣
x+3,则点M(x,﹣![]() x+3),
x+3),
S=![]() ×AB×|yM|=
×AB×|yM|=![]() ×4
×4![]() ×|﹣
×|﹣![]() x+3|,即:S=
x+3|,即:S=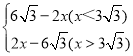 ;
;
②当S=6![]() 时,
时,
∵S=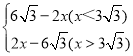
∴![]() 或
或![]()
解得:x=0或x=6![]() ,
,
故点M的坐标为(0,3)或(6![]() ,-3).
,-3).

练习册系列答案
相关题目