题目内容
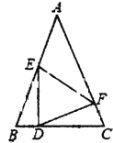
【题目】如图,△ABC和△ECD均为等边三角形,B、C、D三点在一直线上,AD、BE相交于点F,DF=3,AF=4,则线段FE的长为________.
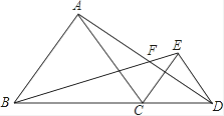
【答案】1
【解析】
首先证△CFF′是等边△,可得![]() ,可证FD=CF+EF=3,根据EF,FC的关系即可求得EF的值.
,可证FD=CF+EF=3,根据EF,FC的关系即可求得EF的值.
如图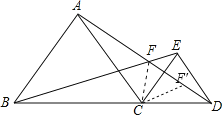
可以认为△BCE是由△ACD逆时针转60°而得;那么CF的起始位是CF′,
∴CF=CF',
∵∠FCF'=60°,
∴△CFF′是等边△,
∴∠BFC=∠CFD=CF'F=60°,
∴CF平分∠DFB.
∵∠CAD+∠ACF=60°,∠ACF+∠FCE=60°,
∴△ACF∽△CEF,
∴![]() ,
,
∵△EFC∽△DF'C,EC=CD,
∴EF=F'D
∴FD=FF'+F'D=CF+EF=3,
解得EF=1.故答案为:1.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目