题目内容
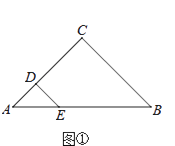
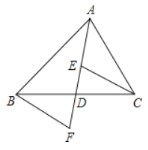
【题目】如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,两线相交于F点.
(1)若∠BAC=60°,∠C=70°,求∠AFB的大小;
(2)若D是BC的中点,∠ABE=30°,求证:△ABC是等边三角形.

【答案】(1)115°;(2)证明见解析
【解析】
(1)根据∠ABF=∠FBD+∠BDF,想办法求出∠FBD,∠BDF即可;
(2)只要证明AB=AC,∠ABC=60°即可;
(1)∵∠BAC=60°,∠C=70°,
∴∠ABC=180°﹣60°﹣70°=50°,
∵BE平分∠ABC,
∴∠FBD=![]() ∠ABC=25°,
∠ABC=25°,
∵AD⊥BC,
∴∠BDF=90°,
∴∠AFB=∠FBD+∠BDF=115°.
(2)证明:∵∠ABE=30°,BE平分∠ABC,
∴∠ABC=60°,
∵BD=DC,AD⊥BC,
∴AB=AC,
∴△ABC是等边三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目