��Ŀ����
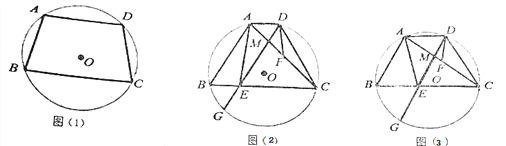
����Ŀ����ͼ�٣��ı���ABCDΪ�����Σ���E��F�ֱ���AB��BC�ϣ��ҡ�EDF=45������֤��AE+CF=EF������֤������
��1����ͼ�ڣ����ı���ABCD�У���ADC=120����DA=DC����DAB=��BCD=90������E��F�ֱ���AB��BC�ϣ��ҡ�EDF=60��������AE��CF��EF֮���������ϵ����֤����IJ��룻
��2����ͼ�ۣ����ı���ABCD�У���ADC=2����DA=DC����DAB���BCD��������E��F�ֱ���AB��BC�ϣ��ҡ�EDF=������ֱ��д��AE��CF��EF֮���������ϵ������֤����

���𰸡���1��AE+CF=EF��֤������������2��![]() �����ɼ�����.
�����ɼ�����.
��������
��1��������нس����̵���ʾ���ٽ�ϵڣ�1���ʵ�֤�����ۣ��ڵڶ��ʿ����ýس����̵ķ���������ȫ�ȣ��Ӷ��ﵽ֤�������
��2��ͬ���������ߣ�ͬ�����м��ɣ�ֱ��д�����룬��֤����
��1��ͼ2���룺AE+CF=EF��
֤������BC���ӳ����Ͻ�ȡCA'=AE������A'D��
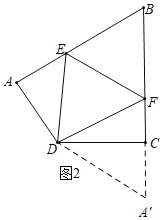
�ߡ�DAB=��BCD=90����
���DAB=��DCA'=90����
�֡�AD=CD��AE=A'C��
���DAE�ա�DCA'��SAS����
��ED=A'D����ADE=��A'DC��
�ߡ�ADC=120����
���EDA'=120����
�ߡ�EDF=60����
���EDF=��A'DF=60����
��DF=DF��
���EDF�ա�A'DF��SAS����
��EF=A'F=FC+CA'=FC+AE��
��2����ͼ3��AE+CF=EF��

֤������BC���ӳ����Ͻ�ȡCA'=AE������A'D��
�ߡ�DAB���BCD��������BCD+��DCA'=180��
���DAB=��DCA'��
�֡�AD=CD��AE=A'C��
���DAE�ա�DCA'��SAS����
��ED=A'D����ADE=��A'DC��
�ߡ�ADC=2����
���EDA'=2����
�ߡ�EDF=����
���EDF=��A'DF=��
��DF=DF��
���EDF�ա�A'DF��SAS����
��EF=A'F=FC+CA'=FC+AE��

 ��У����ϵ�д�
��У����ϵ�д�