Question

【题目】

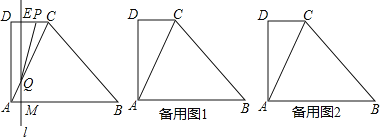
如图，直角梯形ABCD中，AB∥DC，，，．动点M以每秒1个单位长的速度，从点A沿线段AB向点B运动；同时点P以相同的速度，从点C沿折线C-D-A向点A运动．当点M到达点B时，两点同时停止运动．过点M作直线l∥AD，与线段CD的交点为E，与折线A-C-B的交点为Q．点M运动的时间为t（秒）．

（1）当时，求线段的长；

（2）当0＜t＜2时，如果以C、P、Q为顶点的三角形为直角三角形，求t的值；

（3）当t＞2时，连接PQ交线段AC于点R．请探究是否为定值，若是，试求这个定值；若不是，请说明理由．

Answer 1

【答案】（1）1

（2）或

（3）

【解析】

解：（1）过点C作于F，则四边形AFCD为矩形．

∴，．

此时，Rt△AQM∽Rt△ACF．

∴．

即

∴．

（2）∵为锐角，故有两种情况：

①当时，点P与点E重合．

此时，即，∴．

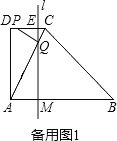
②当时，如备用图1，

此时Rt△PEQ∽Rt△QMA，∴．

由（1）知，，

而，

∴． ∴．

综上所述，或．

（3）为定值．

当＞2时，如备用图2，

．

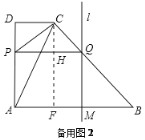
由（1）得，．

∴． ∴．

∴．

∴．

∴四边形AMQP为矩形．

∴PQ∥．

∴△CRQ∽△CAB．

∴．