题目内容
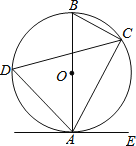
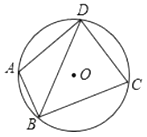
【题目】如图,四边形![]() 为
为![]() 的内接四边形,
的内接四边形,![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,则
,则![]() 的内心与外心之间的距离为________.
的内心与外心之间的距离为________.
【答案】![]()
【解析】
作DF⊥BA于F,连接AD,DC.只要证明△DFA≌△DEC(ASA),推出AF=CE,Rt△BDF≌Rt△BDE(HL),推出AF=BE得到四边形BEDF是正方形,BD是对角线,作△ABC的内切圆,圆心为M,N为切点,连接MN,OM.由切线长定理可知:AN=4,推出ON=5-4=1,由面积法可知内切圆半径为2,在Rt△OMN中,理由勾股定理即可解决问题.
作DF⊥BA于F,连接AD,DC.
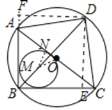
∵BD平分∠ABC,DE⊥BC,DF⊥BA,
∴DF=DE,∠DFB=∠DEB=90°,
∵∠ABC+∠ADC=180°,∠ABC+∠EDF=180°,
∴∠ADC=∠EDF,
∴∠FDA=∠CDE,
∵∠DFA=∠DEC=90°,
∴△DFA≌△DEC(ASA),
∴AF=CE,
∵BD=BD,DF=DE,
∴Rt△BDF≌Rt△BDE(HL),
∴BF=BE,
∴四边形BEDF是正方形,BD是对角线,
∵BD=7![]() ,
,
∴正方形BEDF的边长为7,
由(2)可知:BC=2BE-AB=8,
∴AC=![]() =10,
=10,
作△ABC的内切圆,圆心为M,N为切点,连接MN,OM.
由切线长定理可知:AN=![]() =4,
=4,
∴ON=5-4=1,
由面积法可知内切圆半径为2,
在Rt△OMN中,OM=![]() .
.
∴△ABC的内心与外心之间的距离为![]() ,
,
故答案为![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某校在七年级、八年级开展了阅读文学名著知识竞赛.该校七、八年级各有学生400人,各随机抽取20名学生进行了抽样调查,获得了他们知识竞赛成绩(单位:分),并对数据进行整理、描述和分析.下面给出了部分信息.
a.七年级学生知识竞赛成绩的平均数、中位数、众数、优秀率(80分及以上)如下表所示:
年级 | 平均数 | 中位数 | 众数 | 优秀率 |
七年级 | 84. 2 | 77 | 74 | 45﹪ |
b.八年级学生知识竞赛成绩的扇形统计图如下(数据分为5组,A:50≤x≤59; B:60≤x≤69;C:70≤x≤79;D:80≤x≤89;E:90≤x≤100)

c.八年级学生知识竞赛成绩在D组的是:87 88 88 88 89 89 89 89
根据以上信息,回答下列问题:
(1)八年级学生知识竞赛成绩的中位数是 分;
(2)请你估计该校七、八年级所有学生中达到“优秀”的有多少人?
(3)下列结论:①八年级成绩的众数是89分;②八年级成绩的平均数可能为86分;③八年级成绩的极差可能为50分.其中所有正确结论的序号是 .