题目内容
【题目】某大学生创业团队抓住商机，购进一批干果分装成营养搭配合理的小包装后出售，每袋成本3元．试销期间发现每天的销售量y（袋）与销售单价x（元）之间满足一次函数关系，部分数据如表所示，其中3.5≤x≤5.5，另外每天还需支付其他各项费用80元．
销售单价x（元） | 3.5 | 5.5 |
销售量y（袋） | 280 | 120 |
（1）请直接写出y与x之间的函数关系式；
（2）如果每天获得160元的利润，销售单价为多少元？
（3）设每天的利润为w元，当销售单价定为多少元时，每天的利润最大？最大利润是多少元？
【答案】（1）y＝﹣80x+560；（2）如果每天获得160元的利润，销售单价为4元；（3）当销售单价定为5元时，每天的利润最大，最大利润是240元．
【解析】
（1）根据每天的销售量y（袋）与销售单价x（元）之间满足一次函数关系，可设y=kx+b，再将x=3.5，y=280；x=5.5，y=120代入，利用待定系数法即可求解；（2）根据每天获得160元的利润列出方程（x-3）（-80x+560）-80=160，解方程并结合3.5≤x≤5.5即可求解；（3）根据每天的利润=每天每袋的利润×销售量-每天还需支付的其他费用，列出w关于x的函数解析式，再根据二次函数的性质即可求解．
（1）设y＝kx+b，
将x＝3.5，y＝280；x＝5.5，y＝120代入，
得
，解得
，
则y与x之间的函数关系式为y＝﹣80x+560；
（2）由题意，得（x﹣3）（﹣80x+560）﹣80＝160，
整理，得x2﹣10x+24＝0，
解得x1＝4，x2＝6．
∵3.5≤x≤5.5，
∴x＝4．
答：如果每天获得160元的利润，销售单价为4元；
（3）由题意得：w＝（x﹣3）（﹣80x+560）﹣80
＝﹣80x2+800x﹣1760
＝﹣80（x﹣5）2+240，
∵3.5≤x≤5.5，
∴当x＝5时，w有最大值为240．
故当销售单价定为5元时，每天的利润最大，最大利润是240元．
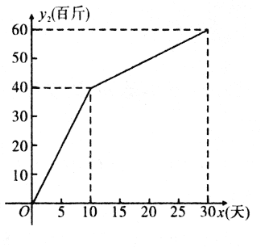
【题目】合肥周谷堆农副产品批发市场某商铺购进一批红薯，通过商店批发和在淘宝网上进行销售．首月进行了销售情况的统计，其中商店日批发量
（百斤）与时间
（为整数，单位：天）的部分对应值如下表所示；在淘宝网上的日销售量
（百斤）与时间（为整数，单位：天）的部分对应值如图所示．
时间 | 0 | 5 | 10 | 150 | 20 | 25 | 30 |
日批发量 | 025 | 40 | 45 | 40 | 25 | 0 |
（1）请你在一次函数、二次函数和反比例函数中，选择合适的函数能反映与的变化规律，求出与之间的函数关系式；
（2）求与之间的函数关系式；
（3）设这个月中，日销售总量为
，求出与之间的函数关系式，并求出当为何值时，日销售总量最大，最大值为多少？
