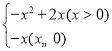题目内容
【题目】已知二次函数y＝﹣x2+bx+c，函数值y与自变量x之间的部分对应值如下表：
x | … | ﹣4 | ﹣1 | 0 | 1 | … |
y | … | ﹣2 | ﹣1 | ﹣2 | ﹣7 | … |
（1）此二次函数图象的对称轴是直线，此函数图象与x轴交点个数为 ．
（2）求二次函数的函数表达式；
（3）当﹣5＜x＜﹣1时，请直接写出函数值y的取值范围．
【答案】（1）2；（2）y＝﹣x2﹣4x﹣2；（3）﹣7＜y＜2.
【解析】
（1）根据抛物线的对称性，x=-4、x=0时的函数值相等，然后列式计算即可得解；
（2）待定系数法求解可得；（3）根据二次函数的性质可得．
解：（1）从表格看，函数的对称轴为：x＝﹣2，
此函数图象与x轴交点个数为2个，一个在x＝﹣3或x＝﹣2之间，一个在x＝﹣2或﹣1之间，故答案为：2个；
（2）函数对称轴为：x＝﹣2＝﹣
，解得：b＝﹣4，
x＝0，y＝﹣2＝c，
故函数的表达式为：y＝﹣x2﹣4x﹣2；
（3）x＝﹣5时，y＝﹣7，x＝1时，y＝﹣7，函数的顶点坐标为：（﹣2，2），
故y的取值范围为：﹣7＜y＜2．
名校课堂系列答案
【题目】已知二次函数
的y与x的部分对应值如表：
x | 1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | 4 | 3 | 0 |
下列结论：①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(
,2),B(
,3)是抛物线上两点,则
,其中正确的个数是 ( )
A. 2B. 3C. 4D. 5
【题目】农经公司以30元/千克的价格收购一批农产品进行销售,为了得到日销售量p(千克)与销售价格x(元/千克)之间的关系，经过市场调查获得部分数据如下表：
销售价格x(元/千克) | 30 | 35 | 40 | 45 | 50 |
日销售量p(千克) | 600 | 450 | 300 | 150 | 0 |
(1)请你根据表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式；
(2)求日销售利润W与X之间的函数表达式.
