题目内容
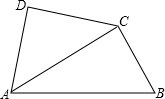
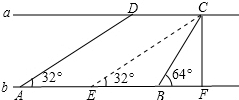
如图,河流两岸a,b互相平行,C,D是河岸a上间隔50m的两个电线杆.某人在河岸b上的A处测得∠DAB=32°,然后沿河岸走了100m到达B处,测得∠CBF=64°,求河流的宽度CF的值?(结果精确到0.1m).参考数据:

| 角度α | sinα | cosα | tanα |
| 32° | 0.53 | 0.85 | 0.62 |
| 64° | 0.9 | 0.44 | 2.05 |

过C作CE∥AD,交AB于E.(如图)(1分)
∵CD∥AE,CE∥AD,
∴四边形AECD是平行四边形,(2分)
∴AE=DC=50,BE=100-50=50,∠CEB=∠DAB=32°,
又∠CBF=64°,
∴∠ECB=32°,
∴BC=BE=50,(4分)
∴在Rt△CFB中,CF=CB•sin64°=50×0.9≈45(米).(4分)
答:河流的宽度CF的值约为45米.(1分)
∵CD∥AE,CE∥AD,
∴四边形AECD是平行四边形,(2分)
∴AE=DC=50,BE=100-50=50,∠CEB=∠DAB=32°,
又∠CBF=64°,
∴∠ECB=32°,
∴BC=BE=50,(4分)
∴在Rt△CFB中,CF=CB•sin64°=50×0.9≈45(米).(4分)
答:河流的宽度CF的值约为45米.(1分)


练习册系列答案
相关题目
 角为30°.
角为30°.