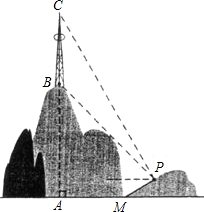
题目内容
如图，两建筑物水平距离BC为30m，从A点测得D点俯角为30°，测得C点的俯角为45°，求这两个建筑物的高度（结果精确到0.1m，
=1.73，
=1.41）
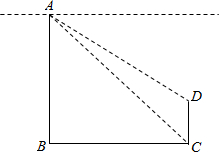
| 3 |
| 2 |
延长CD与水平线交于点E，
∵AE∥BC∴∠EAC=∠ACB=45°，
∵∠B=90°，
∴∠BAC=∠ACB=45°，
∴AB=BC=30，
在Rt△ADE中，tan∠EAD=
，
∴DE=AEtan∠EAD=30tan30°=30×
=10
≈17.3，
∴CD=CE-DE=30-17.3=12.7，
答：建筑物AB、CD的高分别为30m、12.7m．
∵AE∥BC∴∠EAC=∠ACB=45°，
∵∠B=90°，
∴∠BAC=∠ACB=45°，
∴AB=BC=30，
在Rt△ADE中，tan∠EAD=
| DE |
| AE |
∴DE=AEtan∠EAD=30tan30°=30×
| ||
| 3 |
| 3 |
∴CD=CE-DE=30-17.3=12.7，
答：建筑物AB、CD的高分别为30m、12.7m．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
染半径为100米，试问A、B两栋教室是否受到拖拉机噪声的影响若有影响，影响的时间有多少秒？（计算过程中
