Question

如图，在离水面高度为4米的岸上用绳子拉船靠岸，开始时绳子与水面的夹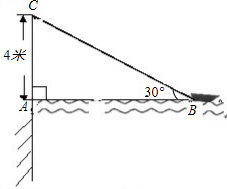角为30°．
求（1）绳子至少有多长？
（2）若此人以每秒0.5米收绳．问：6秒后船向岸边大约移动了多少米？（参考数据：

3

≈1.73）

Answer 1

（1）在Rt△CAB中
∵AC=4（米），∠CBA=30°
∴BC=8（米）．即：绳子至少有8米．（2分）

（2）在Rt△CAB中应用勾股定理得：
AB=

BC2-AC2

=

82-42

=4

3

（1分）
∵

3

≈1.73∴AB=4

3

≈6.92（米）（1分）
设经过拉绳，小船到达D点，在Rt△CAD中
∵AC=4（米），CD=8-0.5×6=5（米）
∴应用勾股定理得：AD=3（米）（2分）
∴DB=AB-AD≈6.92-3=3.92（米）（1分）
答：6秒后船向岸边大约移动了3.92米（1分）．