题目内容
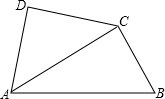
将一副三角板如图拼接:含30°角的三角板(△ABC)的长直角边与含45°角的三角板(△ACD)的斜边恰好重合.已知AB=2
,P是AC上的一个动点,连接DP.
(1)当点P运动到∠ABC的平分线上时,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数.
| 3 |
(1)当点P运动到∠ABC的平分线上时,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数.

(1)在Rt△ABC中,AB=2
,∠BAC=30°
∴BC=
,AC=3.
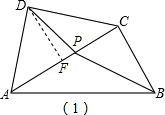
如图(1),作DF⊥AC
∵Rt△ACD中,AD=CD
∴DF=AF=CF=
,
∵BP平分∠ABC
∴∠PBC=30°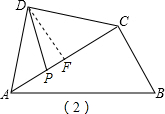
∴CP=BC•tan30°=1
∴PF=
∴DP=
=
.
(2)当P点位置如图(2)所示时,
根据(1)中结论,DF=
,∠ADF=45°
又PD=BC=
∴cos∠PDF=
=
∴∠PDF=30°
∴∠PDA=∠ADF-∠PDF=15°
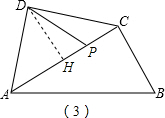
当P点位置如图(3)所示时,
同(2)可得∠PDF=30°.
∴∠PDA=∠ADF+∠PDF=75°.
| 3 |
∴BC=
| 3 |
如图(1),作DF⊥AC
∵Rt△ACD中,AD=CD
∴DF=AF=CF=
| 3 |
| 2 |
∵BP平分∠ABC
∴∠PBC=30°

∴CP=BC•tan30°=1
∴PF=
| 1 |
| 2 |
∴DP=
| PF2+DF2 |
| ||
| 2 |
(2)当P点位置如图(2)所示时,
根据(1)中结论,DF=
| 3 |
| 2 |
又PD=BC=
| 3 |
∴cos∠PDF=
| DF |
| PD |
| ||
| 2 |

∴∠PDF=30°
∴∠PDA=∠ADF-∠PDF=15°
当P点位置如图(3)所示时,
同(2)可得∠PDF=30°.
∴∠PDA=∠ADF+∠PDF=75°.


练习册系列答案
相关题目





 程提前了5天完成,问这两个工程队原计划每天各完成多少土方(坝的土方=坝的横截面的面积×坝的长度)?
程提前了5天完成,问这两个工程队原计划每天各完成多少土方(坝的土方=坝的横截面的面积×坝的长度)?