题目内容
【题目】“创科集团”会议室内的一个长为6米、宽为4米的矩形ABCD墙面需要进行装饰，设计图案如图所示，将矩形ABCD墙面分割成3个区域，中间“十”字形区域甲的宽度均为1米，四个角为四个全等的直角三角形，△AEF，△BGH，△CMN，△DPQ为区域乙，剩下部分为区域丙，其中AE=BG=CN=DP，设EG=HM=NP=FQ=x(米)(1≤x≤3)
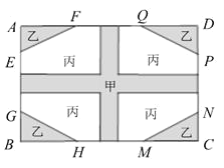
（1）当x=2时，求区域乙的面积；
（2）求区域丙的面积的最大值；
（3）为了图案富有美感，设置区域乙与区域丙的面积之比为1：4，在区域甲、区域乙、区域丙分别嵌贴甲、乙、丙三种不同的装饰板，这三种装饰板每平方米的单价分别为a(百元)，b(百元)，c(百元)(a，b，c均为整数，且6<a<10)，若a+b+c=20，整个墙面嵌贴共花费了150(百元)，求三种装饰板每平方米的单价．
【答案】（1）4；（2）13.5平方米；（3）三种装饰板每平方米的单价分别为9(百元)，7(百元)，4(百元)
【解析】
（1）由x=2可得到AE，AF的长，利用三角形的面积公式求出△AEF的面积，然后可得到区域乙的面积；
（2）利用矩形ABCD的面积和区域甲的面积，求出区域乙的面积，再列出区域丙的面积与x的函数解析式，将函数解析式转化为顶点式，利用二次函数的性质，即可求出区域丙的最大面积；
（3）利用已知求出区域甲、区域乙、区域丙的面积分别为9，3，12，由此可建立关于a，b，c的方程组，解方程组，用含a的代数式表示出c，即可求出a的取值范围，由此可确定出a，b，c的值.
（1）解：当x=2时，AE=1，AF=2，
∴△AEF的面积为1，
∴区域乙的面积为4；
（2）解：矩形ABCD的面积为24， 区域甲的面积为9，
区域乙的面积为
=
x2-5x+12，
设区域丙的面积为y，则y=24-（x2-5x+12）-9，
整理得：y=-(x-5)2+15.5，
∵1≤x≤3，
∴当x=3时，y最大，最大值为13.5，
∴区域丙的面积的最大值为13.5平方米；
（3）解：∵区域乙与区域丙的面积之比为1∶4，区域乙与区域丙的面积之和等于15，
∴区域甲、区域乙、区域丙的面积分别为9，3，12，
根据题意，得 
，
消去b，整理可得：c=10-
a.
∵a，b，c均为整数，且6<a<10，
∴a=9，b=7，c=4，
∴三种装饰板每平方米的单价分别为9(百元)，7(百元)，4(百元).
