Question

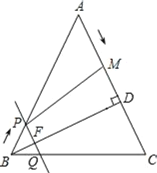
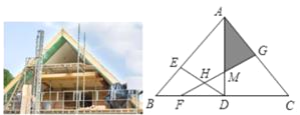
【题目】工人师傅在修茸一人字架屋顶BAC时需要加固，计划焊接三根钢条AD，DE，FG．在如图所示的△ABC中，AB=AC=10，BC=12，AD⊥BC于点D，点E，F，G分别是AB，BD，AC上的点，连接DE，GF，交于点H，GF与AD交于点M，当H为FM的中点，BF∶CF=1∶5，AG：AE=5：7时，△AGM的面积为________．

Answer 1

【答案】

【解析】

过点G作GN∥BC交AD于点N，利用已知条件易证NG∥BC，NG⊥AD，∠B=∠C，∠EAD=∠MAG，同时可求出BD，DC的长，利用勾股定理求出AD的长，结合已知求出BF，CF的长；利用直角三角形的性质，可证得DH=HF=MH，∠ADE=∠FMD=∠AMG，由此可证△BDE∽△CFG，△ADE∽△AMG，利用相似三角形的性质，可求出AM的长及BE与CG的比值；设AG=5m，则AE=7m，用含m的代数式表示出BE，AE的长，由此建立关于m的方程，解方程求出m的值；然后证明△ANG∽△ADC，利用相似三角形的性质求出NG的长，再利用三角形的面积公式求出△AMG的面积.

解：过点G作GN∥BC交AD于点N，

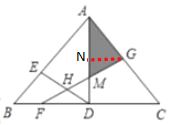
∵AB=AC，AD⊥BC，

∴NG∥BC，NG⊥AD，

∴∠B=∠C，BD=DC=6，∠ADF=90°，∠EAD=∠MAG，

∴；

∵BF:CF=1:5，BC=12，

∴BF+CF=12，

解之：BF=2，CF=10，

在Rt△MDF中，点H是MF的中点，

∴DH=HF=MH，

∴∠BDE=∠CFG，∠ADE=∠FMD=∠AMG，

∵∠BDE=∠CFG，∠B=∠C，

∴△BDE∽△CFG，

∴，

∵∠EAD=∠MAG，∠AMG=∠ADE，

∴△ADE∽△AMG，

∴；

解得：，

设AG=5m，则AE=7m，

∴BE=AB-AE=10-7m，CG=AC-AG=10-5m，

∴，

解得：m=1，

经检验，m=1符合题意，

∴AG=5，

∵NG∥BC，

∴△ANG∽△ADC，

∴ ， 即

解之：NG=3.

∴.

故答案为：.