Question

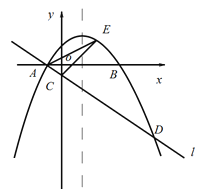
【题目】如图，在平面直角坐标系中，抛物线与轴交于两点（点在点的左侧），经过点的直线与轴负半轴交于点，与抛物线的另一个交点为，且．

（1）直接写出点的坐标，并求直线的函数表达式（其中用含的式子表示）

（2）点是直线上方的抛物线上的动点，若的面积的最大值为，求的值；

（3）设是抛物线的对称轴上的一点，点在抛物线上，当以点为顶点的四边形为矩形时，请直接写出点的坐标．

Answer 1

【答案】（1）A； ；（2）；（3）或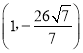

【解析】

（1）令y=0，即，解出x的值即可得出A点的坐标；根据表示出D点的坐标（4，5a），结合A点坐标利用待定系数法即可算出直线解析式；

（2）设点E的坐标，然后结合A点坐标利用待定系数法求出，再利用割补法表示出三角形ACE的面积，根据配方法求最值即可算出a的值；

（3）分别以AD为对角线或AD为边进行分类讨论，再结合矩形的对边平行和一个内角是90°，利用勾股定理计算出a的值，进而确定P点坐标．

（1）令y=0，则，解得x=-1或3，

∵点在点的左侧 ，

∴A；

如图1，作DF⊥x轴于F点，

∴DF∥OC，

∴，

∵，OA=1，

∴OF=4，即D点坐标为（4，5a），将A点和D点坐标代入y=kx+b，得

∴直线

（2）如图1，作EN⊥y轴于点N，设点E，，可得

∴

设AE与y轴交点为M，则M，

∴，NE=m，

∴，

即，

∵的面积的最大值为，

即

解得

（3）由，可得对称轴为x=1，设P点坐标为（1，m），

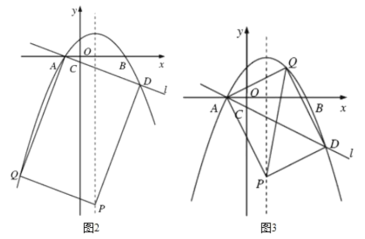
①若AD为矩形一条边，如图2，

则，即，可得Q点横坐标为-4，代入抛物线方程，

可得Q点坐标（-4，21a），∴，

∴P点坐标（1,26a），

∵四边形ADPQ为矩形，∴∠ADP=90°，

∴，

∴，

∵，∴，

∴P点坐标为，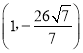

②若AD为矩形的一条对角线，如图3，则AD的中点坐标为，

∴Q点坐标为，进而可得P点坐标为，

∵四边形ADPQ为矩形，∴∠APD=90°，

∴，

∴，

∵，∴，

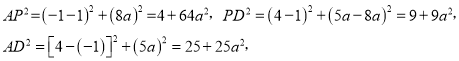
∴P点坐标为

综上可得，P点坐标为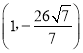或．