题目内容
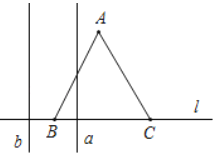
【题目】如图,边长为![]() 的正
的正![]() 的边
的边![]() 在直线
在直线![]() 上,两条距离为
上,两条距离为![]() 的平行直线
的平行直线![]() 和
和![]() 垂直于直线
垂直于直线![]() ,
,![]() 和
和![]() 同时向右移动(
同时向右移动(![]() 的起始位置在
的起始位置在![]() 点),速度均为每秒
点),速度均为每秒![]() 个单位,运动时间为
个单位,运动时间为![]() (秒),直到
(秒),直到![]() 到达
到达![]() 点停止,在
点停止,在![]() 和
和![]() 向右移动的过程中,记
向右移动的过程中,记![]() 夹在
夹在![]() 和
和![]() 间的部分的面积为
间的部分的面积为![]() ,则
,则![]() 关于
关于![]() 的函数图象大致为( )
的函数图象大致为( )
A.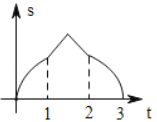 B.
B.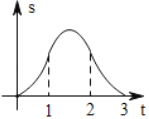
C.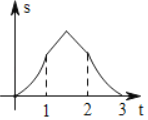 D.
D.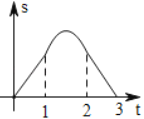
【答案】B
【解析】
依据a和b同时向右移动,分三种情况讨论,求得函数解析式,进而得到当0≤t<1时,函数图象为开口向上的抛物线的一部分,当1≤t<2时,函数图象为开口向下的抛物线的一部分,当2≤t≤3时,函数图象为开口向上的抛物线的一部分.
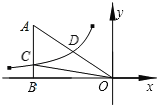
如图①,当0≤t<1时,BE=t,DE=![]() t,
t,
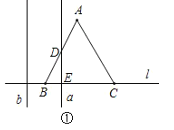
∴s=S△BDE=![]() ×t×
×t×![]() t=
t=![]() t2;
t2;
如图②,当1≤t<2时,CE=2t,BG=t1,

∴DE=![]() (2t),FG=
(2t),FG=![]() (t1),
(t1),
∴s=S五边形AFGED=S△ABCS△BGFS△CDE
=![]() ×2×
×2×![]()
![]() ×(t1)×
×(t1)×![]() (t1)
(t1)![]() ×(2t)×
×(2t)×![]() (2t)
(2t)
=![]() t2+3
t2+3![]() t
t![]() ;
;
如图③,当2≤t≤3时,CG=3t,GF=![]() (3t),
(3t),
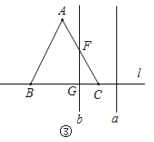
∴s=S△CFG=![]() ×(3t)×
×(3t)×![]() (3t)=
(3t)=![]() t23
t23![]() t+
t+![]() ,
,
综上所述,当0≤t<1时,函数图象为开口向上的抛物线的一部分;当1≤t<2时,函数图象为开口向下的抛物线的一部分;当2≤t≤3时,函数图象为开口向上的抛物线的一部分,
故选B.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目