��Ŀ����
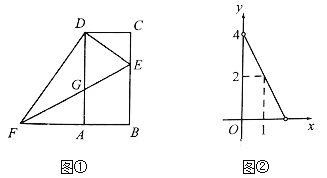
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y��ax2+bx+3��a��0����x��ֱ���A����3��0����B���㣬��y�ύ�ڵ�C�������ߵĶ���E����1��4�����Գ��ύx���ڵ�F��
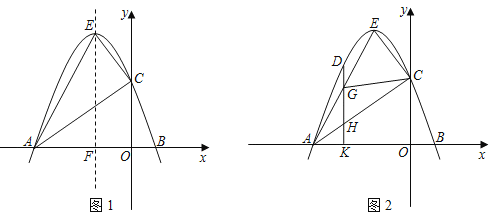
��1����ֱ��д�����������ߺ�ֱ��AE��ֱ��AC�Ľ���ʽ��
��2������AC��AE��CE���жϡ�ACE����״����˵�����ɣ�
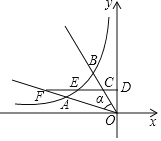
��3����ͼ2����D����������һ���㣬���ĺ�����Ϊm���ҩ�3��m����1������D��DK��x���ڵ�K��DK�ֱ��߶�AE��AC�ڵ�G��H���ڵ�D���˶������У�
��DG��GH��HK�������߶��ܷ���ȣ�����ȣ��������D�����ꣻ������ȣ���˵�����ɣ�
���ڢٵ������£��ж�CG��AE��������ϵ����ֱ��д�����ۣ�
���𰸡���1��y����x2��2x+3��y��2x+6��y��x+3����2��ֱ�������Σ�����������3������ȣ�����2��3������AE��2CG
��������
��1���趥��ʽ����A��������룬�ٻ�Ϊһ��ʽ�����ݳ��������3�������a��ֵ���ɴ˿ɵ������߽���ʽ����ֱ��AE��AC�Ľ���ʽ���ٷֱ�A�㡢E����뼴�����ֱ��AE�Ľ���ʽ����A�㡢C����뼴�����ֱ��AC����ʽ��
��2���ֱ����AC2��CE2��AE2�����ù��ɶ������涨�������ж���
��3���������D��G��H�����꣬��ʾDG��HK��GH���ȣ��ȸ���DG��HK�г��������xֵ���پݴ����DG��HK��GH���ȣ����ɵý⣻�ڷֱ����CG��AE�ij��ȣ����ɵó����ǵ�������ϵ��
�⣺��1�������ߵı���ʽΪ��y��a��x+1��2+4��ax2+2ax+a+4��
��a+4��3����ã�a����1��
�������ߵı���ʽΪ��y����x2��2x+3��
��ֱ��AE�Ľ���ʽΪ��![]() ��
��
����A����3��0����E����1��4�����������һ�κ�������ʽ��
![]() ��
��
��ã�![]() ��
��
��ֱ��AE�ı���ʽΪ��y��2x+6��
��ֱ��AC�Ľ���ʽΪ��![]() ��
��
����A����3��0����C��0��3�����������һ�κ�������ʽ��
![]() ��
��
��ã�![]() ��
��
��ֱ��AC�ı���ʽΪ��y��x+3��
��2����A��C��E������ֱ�Ϊ������3��0������0��3��������1��4����
��AC2��![]() =18��CE2��
=18��CE2��![]() =2��AE2��
=2��AE2��![]() =20��
=20��
��AC2+CE2��AE2�����ACEΪֱ�������Σ�
��3�������D��G��H������ֱ�Ϊ����x����x2��2x+3������x��2x+6������x��x+3����
DG����x2��2x+3��2x��6����x2��4x��3��HK��x+3��GH��2x+6��x��3��x+3��
��DG��HKʱ����x2��4x��3��x+3����ã�x����2��3����ȥ��3������x����2��
��x����2ʱ��DG��HK��GH��1��
��DG��GH��HK�������߶����ʱ����D������Ϊ������2��3����
���ɢٵĵ�G������Ϊ������2��2��
CG��![]() ��
��![]() ��AE��
��AE��![]() ��2
��2![]() ��
��
��AE��2CG��

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�����Ŀ�����κ���![]() ��
��![]() ��
��![]() ��
��![]() ��������
Ϊ��������![]() ���е�
���е�![]() ��
��![]() �IJ��ֶ�Ӧֵ���±���
�IJ��ֶ�Ӧֵ���±���
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
���½��ۣ�
�ٶ��κ���![]() ����СֵΪ
����СֵΪ![]() ��
��
�ڵ�![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
�۶��κ���![]() ��ͼ����
��ͼ����![]() ��ֻ��һ�����㣻
��ֻ��һ�����㣻
�ܵ�![]() ʱ��
ʱ��![]() .
.
������ȷ�Ľ����У� ����
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
����Ŀ���Ϸʰٴ����½���40̨�յ�����60̨����䣬�ƻ�����������ļס����������������ۣ�����70̨���������꣬30̨���������꣮�������������������ֵ���ÿ̨������Ԫ�����±���
�յ��� | ����� | |
�������� | 200 | 170 |
�������� | 160 | 150 |
�輯�ŵ������������x̨�յ���������������100̨������������Ϊy��Ԫ����
��1����y����x�ĺ�����ϵʽ�������x��ȡֵ��Χ��
��2��Ϊ�˴��������ž������Լ�������Ŀյ���ÿ̨����aԪ���ۣ��������������䣬����������ÿ̨�յ�����������Ȼ���ڼ����������۵�ÿ̨�����������ʸü���Ӧ�������Ƶ��䷽��������ʹ������ﵽ���