题目内容
【题目】如图,已知在平面直角坐标系xOy中,点A(4,0)是抛物线y=ax2+2x-c上的一点,将此抛物线向下平移6个单位后经过点B(0,2),平移后所得的新抛物线的顶点记为C,新抛物线的对称轴与线段AB的交点记为P.
(1)求平移后所得到的新抛物线的表达式,并写出点C的坐标;
(2)求∠CAB的正切值;
(3)如果点Q是新抛物线对称轴上的一点,且△BCQ与△ACP相似,求点Q的坐标.

【答案】(1)y=-x2+2x+2,点C的坐标为(1,3);(2)tan∠CAB=![]() ;(3)Q(1,
;(3)Q(1,![]() ).
).
【解析】
(1)先根据点B(0,2)向上平移6个单位得到点B'(0,8),将A(4,0),B'(0,8)分别代入y=ax2+2x-c,得原抛物线为y=-x2+2x+8,向下平移6个单位后所得的新抛物线为y=-x2+2x+2,据此求得顶点C的坐标;
(2)根据A(4,0),B(0,2),C(1,3),得到AB2=20,AC2=18,BC2=2,进而得出AB2=AC2+BC2,根据∠ACB=90°,求得tan∠CAB的值即可;
(3)先设抛物线的对称轴x=1与x轴交于点H,根据![]() =
=![]() ,求得PH=
,求得PH=![]() AH=
AH=![]() ,进而得到P(1,
,进而得到P(1,![]() ),再由HA=HC=3,得∠HCA=45°,根据当点Q在点C下方时,∠BCQ=∠ACP,因此△BCQ与△ACP相似分两种情况,根据相似三角形的性质即可得到点Q的坐标.
),再由HA=HC=3,得∠HCA=45°,根据当点Q在点C下方时,∠BCQ=∠ACP,因此△BCQ与△ACP相似分两种情况,根据相似三角形的性质即可得到点Q的坐标.
解:(1)点B(0,2)向上平移6个单位得到点B'(0,8),
将A(4,0),B'(0,8)分别代入y=ax2+2x-c,得
![]() ,
,
解得![]() ,
,
∴原抛物线为y=-x2+2x+8,向下平移6个单位后所得的新抛物线为y=-x2+2x+2,
∴顶点C的坐标为(1,3);
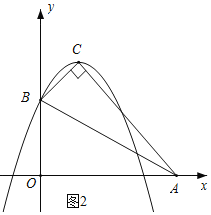
(2)如图2,由A(4,0),B(0,2),C(1,3),得
AB2=20,AC2=18,BC2=2,
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴tan∠CAB=![]() =
=![]() =
=![]() ;
;
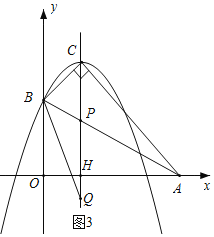
(3)如图3,设抛物线的对称轴x=1与x轴交于点H,
由![]() =
=![]() =
=![]() ,得PH=
,得PH=![]() AH=
AH=![]() ,
,
∴P(1,![]() ),
),
由HA=HC=3,得∠HCA=45°,
∴当点Q在点C下方时,∠BCQ=∠ACP,
因此△BCQ与△ACP相似分两种情况:
①如图3,当![]() =
=![]() 时,
时,![]() =
=![]() ,
,
解得CQ=4,
此时Q(1,-1);
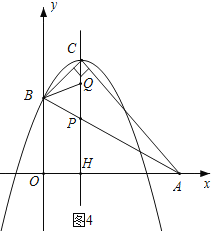
②如图4,当![]() =
=![]() 时,
时,![]() =
=![]() ,
,
解得CQ=![]() ,
,
此时Q(1,![]() ).
).

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案【题目】如图,已知y是x(x>0)的函数,表1中给出了几组x与y的对应值:
表1:
x | … |
| 1 |
| 2 |
| 3 | … |
y | … | 6 | 3 | 2 |
|
| 1 | … |
⑴以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出![]() 的值;
的值;
⑵如果一次函数图像与⑴中图像交于(1,3)和(3,1)两点,在第一、四象限内当x在什么范围时,一次函数的值小于⑴中函数的值?请直接写出答案.