��Ŀ����
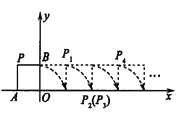
����Ŀ������ʦ��һ�����Ǹ�����ѧ����ѧ������֮�أ�����һ����ѧС�ֶӴ��人վ�³����ƻ������г����人վ������ʦ��һ���У�����һ��ʱ������й�����Ʒ�������人վ�����ǰ���С�������г���ԭ�ٷ��أ�ʣ�µij�Ա�ٶȲ�������ʦ��һ����ǰ����С��ȡ����Ʒ�ij˳���ϳ��ӣ�ȡ��Ʒ���ȳ�ʱ����Բ��ƣ���С�����������г��Ӻ��Գ������������ʻ10���Ӻ������³����ڴ��ڼ䣬���г��ӷ��������ӵ��30���Ӻ�ͨ�ָ������������ԭ�ٿ�������ʦ��һ���У����ճ�������г���ͬʱ��������г��Ӻ�С����ʻʱ��Ϊt���ӣ����人վ����sǧ�ף�s��t�ĺ�����ϵ��ͼ��ʾ����ӵڶ�������������³�������������_____����.

���𰸡�10��
��������
��ǰ30����ͼ���С����ʻ·��֪���г��ٶ���ÿ����![]() ǧ�ף����г������յ���ʱ90���ӣ����30���ӵ���Ŀ�ĵأ����ٶ���ÿ����0.8ǧ�ף������һ������ʱ�䣬�����Ƶ����ڶ�������ʱ�䣬�Ӷ�������ڶ�������������³�������ʱ�䣮
ǧ�ף����г������յ���ʱ90���ӣ����30���ӵ���Ŀ�ĵأ����ٶ���ÿ����0.8ǧ�ף������һ������ʱ�䣬�����Ƶ����ڶ�������ʱ�䣬�Ӷ�������ڶ�������������³�������ʱ�䣮
�⣺�۲�ͼ���֪�����г��ٶ�=8��30= ![]() ǧ��/�֣�
ǧ��/�֣�
�����г����ﻪ��ʦ��һ����ʱ�䣺24��![]() =90���ӣ�
=90���ӣ�
�������ﻪ��ʦ��һ������ʱ90-30-30=30���ӣ�
�����ٶ�24��30=0.8ǧ��/�֣�
�����г�����x���ӵ�һ�����������������![]() x��0.8(x30)��
x��0.8(x30)��
���x=45��
�����г�����y���ӵڶ�����������
![]() y��0.8(45+1030)��
y��0.8(45+1030)��
���y=75��
���Եڶ�������������³�������������ʱ��Ϊ45+10+30-75=10�����ӣ���
�ʴ�Ϊ��10��

 ��У����ϵ�д�
��У����ϵ�д�