题目内容
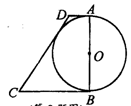
如图,以AB为直径的⊙O与AD、DC、BC均相切,若AB=BC=4,则OD的长度为
A.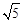 B.
B.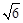 C.
C.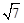 D.2
D.2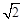

A.
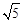 B.
B.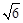 C.
C.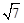 D.2
D.2
A
过D作DF⊥BC,连接OD,有切线长定理和勾股定理求出AD的长,在直角三角形ADO中再由勾股定理求出OD的长即可.
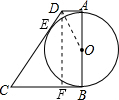
解:过D作DF⊥BC,连接OD,设AD为x,
由题意知:四边形ADFB为矩形,
∴AD=BF=x,
∴CF=4-x,
有切线长定理得:CE=CB=4,
∴CD=4+x,
在Rt△DFC中,42+(4-x)2=(4+x)2,
解得:x=1
∴AD=1,
∴在Rt△ADO中,AO=2,AD=1,AD=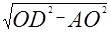
∴OD= ,
,
故选A.
本题考查了矩形的性质、切线长定理、以及勾股定理,解题的关键是作辅助线构造直角三角形.

解:过D作DF⊥BC,连接OD,设AD为x,
由题意知:四边形ADFB为矩形,
∴AD=BF=x,
∴CF=4-x,
有切线长定理得:CE=CB=4,
∴CD=4+x,
在Rt△DFC中,42+(4-x)2=(4+x)2,
解得:x=1
∴AD=1,
∴在Rt△ADO中,AO=2,AD=1,AD=
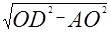
∴OD=
 ,
,故选A.
本题考查了矩形的性质、切线长定理、以及勾股定理,解题的关键是作辅助线构造直角三角形.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 的图像过点P,则
的图像过点P,则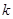 = .
= .
 的两个根,则它们的圆心距
的两个根,则它们的圆心距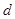 的取值范围是 .
的取值范围是 .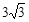 cm
cm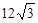 cm
cm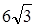 cm
cm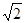 、
、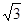 ,则∠BAC的度数为 _____.
,则∠BAC的度数为 _____.