Question

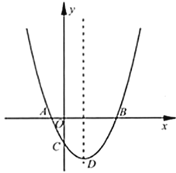
【题目】在平面直角坐标系中，把与轴交点相同的二次函数图像称为“共根抛物线”．如图，抛物线的顶点为，交轴于点、（点在点左侧），交轴于点．抛物线与是“共根抛物线”，其顶点为．

（1）若抛物线经过点，求对应的函数表达式；

（2）当的值最大时，求点的坐标；

（3）设点是抛物线上的一个动点，且位于其对称轴的右侧．若与相似，求其“共根抛物线”的顶点的坐标．

Answer 1

【答案】（1）；（2）点；（3）或或或

【解析】

（1）由“共根抛物线”定义可知抛物线经过抛物线与x轴交点，故根据抛物线可求AB两点坐标进而由交点式设为，将点代入，即可求出解；

（2）由抛物线对称性可知PA=PB，∴，根据三角形两边之差小于第三边可知当当、、三点共线时，的值最大，而P点在对称轴为上，由此求出点P坐标；

（3）根据点ABC坐标可证明△ABC为直角三角形，与相似，分两种情况讨论：当、时，分别利用对应边成比例求解即可．

解：（1）当时，，解得，．

∴、、．

由题意得，设对应的函数表达式为，

又∵经过点，

∴，

∴．

∴对应的函数表达式为．

（2）∵、与轴交点均为、，

∴、的对称轴都是直线．

∴点在直线上．

∴．

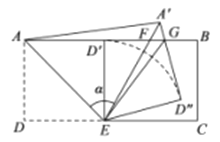
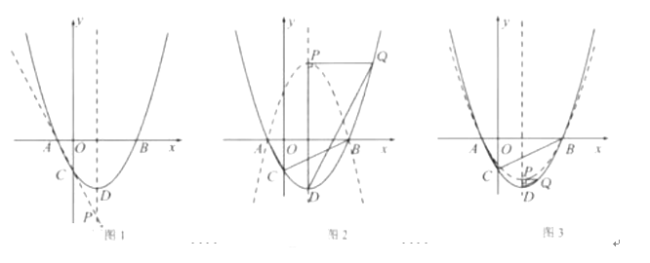
如图1，当、、三点共线时，的值最大，

此时点为直线与直线的交点．

由、可求得，直线对应的函数表达式为．

∴点．

（3）由题意可得，，，，

因为在中，，故．

由，得顶点．

因为的顶点P在直线上，点Q在上，

∴不可能是直角．

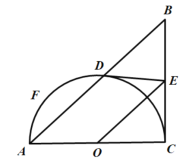
第一种情况：当时，

①如图2，当时，则得．

设，则，

∴．

由得，解得．

∵时，点Q与点P重合，不符合题意，

∴舍去，此时．

②如图3，当时，则得．

设，则．

∴．

由得，解得（舍），此时．

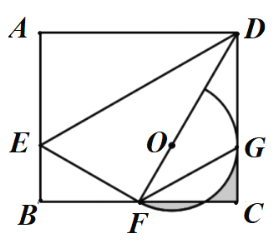
第二种情况：当时，

①如图4，当时，则得．

过Q作交对称轴于点M，∴．

∴．由图2可知，

∴．

∴，又，代入得．

∵点，

∴点．

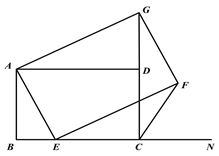
②如图5，当时，则．

过Q作交对称轴于点M，

∴，则．

由图3可知，，

∴，，

∴．

又，代入得．

∵点，

∴点，

综上所述，或或或．