题目内容
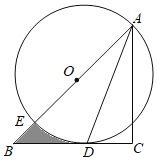
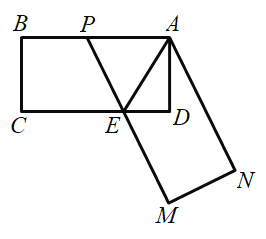
【题目】如图,在矩形ABCD中,![]() ,
,![]() ,把△EAD沿AE折叠,使点D恰好落在AB边上的
,把△EAD沿AE折叠,使点D恰好落在AB边上的![]() 处,再将
处,再将![]() 绕点E顺时针旋转
绕点E顺时针旋转![]() ,得到
,得到![]() ,使得
,使得![]() 恰好经过
恰好经过![]() 的中点F.
的中点F.![]() 交AB于点G,连接
交AB于点G,连接![]() 有如下结论:①
有如下结论:①![]() 的长度是
的长度是![]() ;②弧
;②弧![]() 的长度是
的长度是![]() ;③
;③![]() ;④
;④![]() .上述结论中,所有正确的序号是________.
.上述结论中,所有正确的序号是________.
【答案】①②④
【解析】
①先根据图形翻折变换的性质以及勾股定理得出![]()
![]() 的长,再根据勾股定理求出EF的长,即可求解;
的长,再根据勾股定理求出EF的长,即可求解;
②利用特殊角的三角函数求得![]() ,从而求得
,从而求得![]() ,根据弧长公式即可求解;
,根据弧长公式即可求解;
③由于![]() 不是等边三角形,得出
不是等边三角形,得出![]() ,从而说明
,从而说明![]() 和
和![]() 不是全等三角形;
不是全等三角形;
④先利用“HL”证得![]()
![]()
![]() ,求得
,求得![]() ,再求得
,再求得![]() ,从而推出
,从而推出![]() .
.
①在矩形ABCD中,![]() ,
,
∵△ADE翻折后与△AD′E重合,
∴AD′=AD,D′E=DE,![]() ,
,
∴四边形ADED′是正方形,
∴AD′=AD=D′E=DE=![]() ,
,
∴AE=![]() ,
,
将![]() 绕点E顺时针旋转
绕点E顺时针旋转![]() ,得到
,得到![]() ,
,
∴![]()
![]()
![]() ,
,![]() =
=![]() =
=![]() ,
,![]() ,
,
∵点F是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,故①正确;
,故①正确;
②由①得![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴弧![]() 的长度是
的长度是![]() ,故②正确;
,故②正确;
③在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() 不是等边三角形,
不是等边三角形,
∴![]() ,
,
∴![]() 和
和![]() 不是全等三角形,故③错误;
不是全等三角形,故③错误;
④在![]() 和
和![]() 中,
中,![]() ,
,![]() 公共,
公共,
∴![]()
![]()
![]() (HL),
(HL),
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ,故④正确;
,故④正确;
综上,①②④正确,
故答案为:①②④.

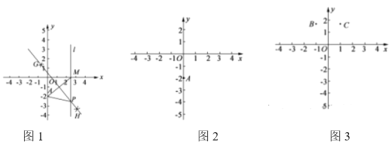
【题目】如图1,在平面直角坐标系中,点A的坐标是![]() ,在x轴上任取一点M.连接AM,分别以点A和点M为圆心,大于
,在x轴上任取一点M.连接AM,分别以点A和点M为圆心,大于![]() 的长为半径作弧,两弧相交于G,H两点,作直线GH,过点M作x轴的垂线l交直线GH于点P.根据以上操作,完成下列问题.
的长为半径作弧,两弧相交于G,H两点,作直线GH,过点M作x轴的垂线l交直线GH于点P.根据以上操作,完成下列问题.
探究:
(1)线段PA与PM的数量关系为________,其理由为:________________.
(2)在x轴上多次改变点M的位置,按上述作图方法得到相应点P的坐标,并完成下列表格:
M的坐标 | … |
|
|
|
| … |
P的坐标 | … |
|
| … |
猜想:
(3)请根据上述表格中P点的坐标,把这些点用平滑的曲线在图2中连接起来;观察画出的曲线L,猜想曲线L的形状是________.
验证:
(4)设点P的坐标是![]() ,根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
,根据图1中线段PA与PM的关系,求出y关于x的函数解析式.
应用:
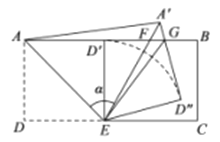
(5)如图3,点![]() ,
,![]() ,求点D的纵坐标
,求点D的纵坐标![]() 的取值范围.
的取值范围.