题目内容
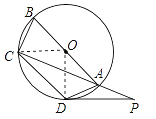
【题目】如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.

(1)若AB=4,求弧CD的长.
(2)若弧BC=弧AD,AD=AP. 求证:PD是⊙O的切线.
【答案】(1)π;(2)见解析
【解析】试题分析:(1)连接OC,OD,由圆周角定理得到∠COD=2∠CAD,∠CAD=45°,于是得到∠COD=90°,根据弧长公式即可得到结论;
(2)由已知条件得到∠BOC=∠AOD,由圆周角定理得到∠AOD=45°,根据等腰三角形的性质得到∠ODA=∠OAD,求得∠ADP=![]() CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到结论.
CAD=22.5°,得到∠ODP=∠ODA+∠ADP=90°,于是得到结论.
试题解析:(1)连接OC,OD,
∵∠COD=2∠CAD,∠CAD=45°
∴∠COD=90°
∵AB=4 ∴![]()
∴![]() 的长
的长![]()
(2)∵![]() ∴∠BOC=∠AOD,
∴∠BOC=∠AOD,
∵∠COD=90°,∴∠AOD=![]()
∵OA=OD,∴∠ODA=∠OAD,
∵∠AOD+∠ODA+∠OAD=180° ∴∠ODA=![]() ,
,
∵AD=AP, ∴∠ADP=∠APD
∵∠CAD=∠ADP+∠APD, ∠CAD=45°,
∴∠ADP=![]() ∠CAD=22.5°,
∠CAD=22.5°,
∴∠ODP=∠ODA+∠ADP=90°
又∵OD是半径,∴PD是⊙O的切线

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】(10分)学校组织学生参加综合实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价定为多少元?