题目内容
【题目】如图（1），已知正方形ABCD，E是线段BC上一点，N是线段BC延长线上一点，以AE为边在直线BC的上方作正方形AEFG.
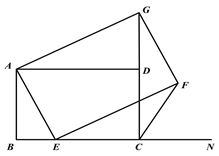
图（1） 图（2）
（1）连接GD，求证：DG＝BE；
（2）连接FC，求∠FCN的度数；
（3）如图（2），将图（1）中正方形ABCD改为矩形ABCD，AB=m，BC=n（m、n为常数），E是线段BC上一动点（不含端点B、C），以AE为边在直线BC的上方作矩形AEFG，使顶点G恰好落在射线CD上．判断当点E由B向C运动时，∠FCN的大小是否总保持不变？若∠FCN的大小不变，请用含m、n的代数式表示tan∠FCN的值；若∠FCN的大小发生改变，请画图说明.
【答案】（1）证明见解析；（2）∠FCN=45°；（3）当点E由B向C运动时，∠FCN的大小总保持不变，tan∠FCN=
．
【解析】
金博士一点全通系列答案
【题目】某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分均为
分.前
名选手的得分如下：根据规定，笔试成绩和面试成绩分别按一定的百分比折合成综合成绩（综合成绩的满分仍为分），现得知
号选手的综合成绩为
分.
序号 |
|
|
|
笔试成绩/分 |
|
|
|
面试成绩/分 |
|
|
|
（1）求笔试成绩和面试成绩各占的百分比：
（2）求出其余两名选手的综合成绩，并以综合成绩排序确定这三名选手的名次。
【题目】某校九年级（1）班全体学生2018年初中毕业体育学业考试成绩统计表如下：
成绩/分 | 45 | 49 | 52 | 54 | 55 | 58 | 60 |
人数 | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根据上表中信息判断，下列结论中错误的是（ ）
A.该班一共有40名同学
B.该班学生这次考试成绩的众数是55分
C.该班学生这次考试成绩的中位数是55分
D.该班学生这次考试成绩的平均数是55分
【题目】学校准备从甲乙两位选手中选择一位选手代表学校参加所在地区的汉字听写大赛，学校对两位选手从表达能力、阅读理解、综合素质和汉字听写四个方面做了测试，他们各自的成绩（百分制）如表：
选手 | 表达能力 | 阅读理解 | 综合素质 | 汉字听写 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
（1）由表中成绩已算得甲的平均成绩为80.25，请计算乙的平均成绩，从他们的这一成绩看，应选派谁；
（2）如果表达能力、阅读理解、综合素质和汉字听写分别赋予它们2、1、3和4的权，请分别计算两名选手的平均成绩，从他们的这一成绩看，应选派谁．
