Question

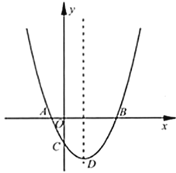
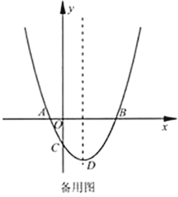
【题目】如图，抛物线顶点A的坐标为（1,4），抛物线与x轴相交于B、C两点，与y轴交于点E（0,3）．

（1）求抛物线的表达式；

（2）已知点F（0，-3），在抛物线的对称轴上是否存在一点P，使得EP+FP最小，如果存在，求出点P的坐标；如果不存在，请说明理由．

Answer 1

【答案】（1）y=x2+2x+3；（2）存在，P(1,0)，理由见解析；

【解析】

（1）根据顶点式可求得抛物线的表达式；
（2）根据轴对称的最短路径问题，作E关于对称轴的对称点E'，连接E'F交对称轴于P，此时EP+FP的值最小，先求E'F的解析式，它与对称轴的交点就是所求的点P；

（1）设抛物线的表达式为：y=a(x1)2+4，

把(0,3)代入得：3=a(01)2+4，

解得：a=1，

∴抛物线的表达式为：y=(x1)2+4=x2+2x+3；

（2）存在，

作E关于对称轴的对称点E′，连接E′F交对称轴于P，此时EP+FP的值最小，

∵E(0,3)，

∴E′(2,3)，

易得E′F的解析式为：y=3x3，

当x=1时，y=3×13=0，

∴P(1,0)．