题目内容
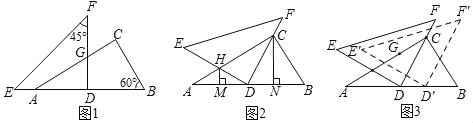
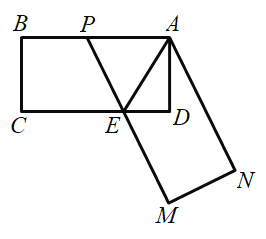
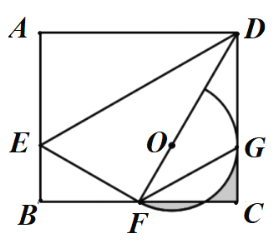
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 上的一点,连接
上的一点,连接![]() ,将△
,将△![]() 进行翻折,恰好使点
进行翻折,恰好使点![]() 落在
落在![]() 的中点
的中点![]() 处,在
处,在![]() 上取一点
上取一点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作半圆与
的长为半径作半圆与![]() 相切于点
相切于点![]() ;若
;若![]() ,则图中阴影部分的面积为 ____ .
,则图中阴影部分的面积为 ____ .
【答案】![]() .
.
【解析】
连接OG,证明△DOG∽△DFC,得出![]() ,设OG=OF=r,进而求出圆的半径,再证明△OFQ为等边三角形,则可由扇形的面积公式和三角形的面积公式求出答案.
,设OG=OF=r,进而求出圆的半径,再证明△OFQ为等边三角形,则可由扇形的面积公式和三角形的面积公式求出答案.
解:连接OG,过O点作OH⊥BC于H点,设圆O与BC交于Q点,如下图所示:

设圆的半径为r,
∵CD是圆的切线,
∴OG⊥CD,
∴△DOG∽△DFC,
∴![]() ,由翻折前后对应的线段相等可得DF=DA=4,
,由翻折前后对应的线段相等可得DF=DA=4,
∵F是BC的中点,∴CF=BF=2,代入数据:
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴∠ODG=30°,∴∠DFC=60°,
且OF=OQ,∴△OFQ是等边三角形,
∴∠DOQ=180°-60°=120°,
同理△OGQ也为等边三角形,
∴OH=![]() ,且S扇形OGQ=S扇形OQF
,且S扇形OGQ=S扇形OQF
∴![]()
![]()
![]() .
.
故答案为:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】在初中阶段的函数学习中,我们经历了列表、描点、连线画函数图象,并结合图象研究函数性质的过程.以下是我们研究函数![]() 性质及其应用的部分过程,请按要求完成下列各小题.
性质及其应用的部分过程,请按要求完成下列各小题.
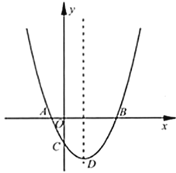
(1)请把下表补充完整,并在图中补全该函数图象;
| … | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … |
|
|
| -3 | 0 | 3 |
|
|
| … |
(2)根据函数图象,判断下列关于该函数性质的说法是否正确,正确的在相应的括号内打“√”,错误的在相应的括号内打“×”;
①该函数图象是轴对称图形,它的对称轴为y轴;( )
②该函数在自变量的取值范围内,有最大值和最小值,当![]() 时,函数取得最大值3;当
时,函数取得最大值3;当![]() 时,函数取得最小值-3;( )
时,函数取得最小值-3;( )
③当![]() 或
或![]() 时,y随x的增大而减小;当
时,y随x的增大而减小;当![]() 时,y随x的增大而增大;( )
时,y随x的增大而增大;( )
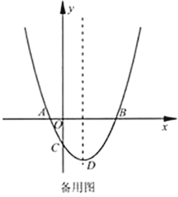
(3)已知函数![]() 的图象如图所示,结合你所画的函数图象,直接写出不等式
的图象如图所示,结合你所画的函数图象,直接写出不等式![]() 的解集(保留1位小数,误差不超过0.2).
的解集(保留1位小数,误差不超过0.2).