题目内容
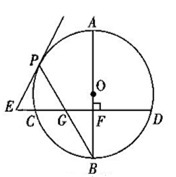
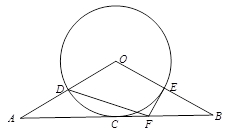
如图,已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG,
(1)求证:直线EP为⊙O的切线;
(2)点P在劣弧AC上运动,其他条件不变,若BG²=BF·BO.试证明BG=PG.
(3)在满足(2)的条件下,已知⊙O的半径为3,sinB=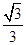 .求弦CD的长.
.求弦CD的长.
(1)求证:直线EP为⊙O的切线;
(2)点P在劣弧AC上运动,其他条件不变,若BG²=BF·BO.试证明BG=PG.
(3)在满足(2)的条件下,已知⊙O的半径为3,sinB=
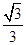 .求弦CD的长.
.求弦CD的长.
(1)(2)证法见解析;(3)CD=4

试题分析:(1)连接OP,根据切线的判定定理证OP⊥EP即可;(2)连接OG根据相似三角形的判定定理证
△BFG∽△BGO得∠BFG=∠BGO=90°再由垂径定理得BG=PG;(3)由sinB=
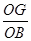 =
=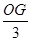 =
=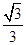 得OG=
得OG=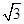 ∴BG=
∴BG=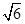 ,由BG²=BF·BO得BF=2,∴OF=1由勾股定理得DF=2
,由BG²=BF·BO得BF=2,∴OF=1由勾股定理得DF=2 再由垂径定理得CD=4
再由垂径定理得CD=4
试题解析:

(1)连接OP,∵OP="OB" ∴∠OPB=∠B
∵EP=EG ∴∠EPG=∠EGP 又∵∠EGP=∠BGF
∠BGF+∠B=90°
∴∠OPB+∠EPG=90° OP过圆心,
∴直线EP为⊙O的切线;
∵BG²=BF·BO ∴
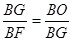 又∵∠GBF=∠OBG
又∵∠GBF=∠OBG∴△GBF∽△OBG ∴∠GFB=∠OGB=90°
∴OG⊥PB , OG过圆心
BG=PG.
在Rt△OGB中,sinB=
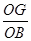 =
=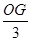 =
=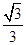
∴OG=
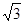
由射影定理得:OG2="OF" OB
∴(
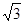 )2=OF×3 OF=1
)2=OF×3 OF=1在Rt△OFB中 FD=2

∵OF⊥CD FO过圆心
∴FD=FC ∴CD="2" FD=4


练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
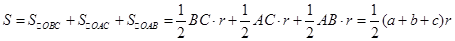 .
.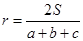 .
.
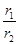 的值.
的值.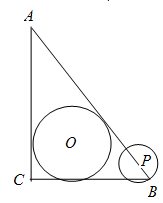
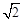 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 .
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 .
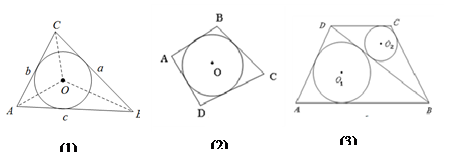
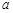 与b,如图⑴;②可以画出∠AOB的平分线OP,如图⑵所示;③可以检验工件的凹面是否为半圆,如图⑶所示;④可以量出一个圆的半径,如图⑷所示.这四种说法正确的个数有 ( )
与b,如图⑴;②可以画出∠AOB的平分线OP,如图⑵所示;③可以检验工件的凹面是否为半圆,如图⑶所示;④可以量出一个圆的半径,如图⑷所示.这四种说法正确的个数有 ( )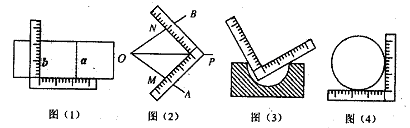
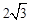 ;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=
;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=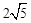 ;⑤当点D从点A运动到点B时,线段EF扫过的面积是
;⑤当点D从点A运动到点B时,线段EF扫过的面积是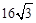 .其中正确结论的序号是 .
.其中正确结论的序号是 .
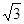 ≈1.7,保留三个有效数字);
≈1.7,保留三个有效数字);