题目内容
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.
(1)求圆形区域的面积;
(2)某时刻海面上出现-渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,求观测点B到A船的距离.(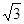 ≈1.7,保留三个有效数字);
≈1.7,保留三个有效数字);
(3)当渔船A由(2)中位置向正西方向航行时,是否会进入海洋生物保护区?通过计算回答。
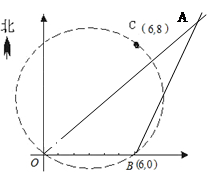
(1)求圆形区域的面积;
(2)某时刻海面上出现-渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,求观测点B到A船的距离.(
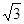 ≈1.7,保留三个有效数字);
≈1.7,保留三个有效数字);(3)当渔船A由(2)中位置向正西方向航行时,是否会进入海洋生物保护区?通过计算回答。

(1)25π;(2)16.2;(3)A船不会进入海洋生物保护区.
试题分析:(1)连接CB,CO,则CB∥y轴,由圆周角定理、勾股定理得OC=
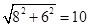 ,则半径OO′=5,S⊙O′=π•52=25π.
,则半径OO′=5,S⊙O′=π•52=25π.(2)过点A作AD⊥x轴于点D,依题意,得∠BAD=30°,在Rt△ABD中,设BD=x,则AB=2x,由勾股定理AD=
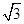 x,根据图形得到OD=OB+BD=6+x,故AB=2x=6(
x,根据图形得到OD=OB+BD=6+x,故AB=2x=6(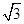 +1)≈16.2
+1)≈16.2(3)过点A作AG⊥y轴于点G.过点O′作O′E⊥OB于点E,并延长EO′交AG于点F.由垂径定理得,OE=BE=3.在Rt△OO′E中,由勾股定理得,O′E=4.所以O′F=9+3
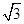 -4=5+3
-4=5+3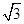 >5.
>5.(1)连接CB,CO,则CB∥y轴,
∴∠CBO=90°,
设O′为由O、B、C三点所确定圆的圆心.
则OC为⊙O′的直径.
由已知得OB=6,CB=8,由勾股定理得OC=
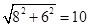
半径OO′=5,S⊙O′=π•52=25π.
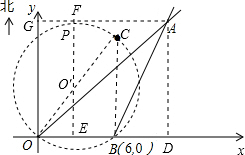
(2)过点A作AD⊥x轴于点D,依题意,得∠BAD=30°,
在Rt△ABD中,设BD=x,则AB=2x,
由勾股定理得,AD=
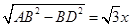 ,
,由题意知:OD=OB+BD=6+x,在Rt△AOD中,OD=AD,6+x=
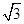 x
x∴x=3(
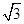 +1),
+1),∴AB=2x=6(
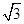 +1)≈16.2
+1)≈16.2(3)过点A作AG⊥y轴于点G.
过点O′作O′E⊥OB于点E,并延长EO′交AG于点F.
由(1)知,OO′=5,由垂径定理得,OE=BE=3.
∴在Rt△OO′E中,由勾股定理得,O′E=4
∵四边形FEDA为矩形.
∴EF=DA,而AD=
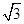 x=9+3
x=9+3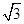
∴O′F=9+3
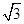 -4=5+3
-4=5+3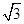 >5,
>5,∴直线AG与⊙O′相离,A船不会进入海洋生物保护区.
考点: 1.勾股定理的应用;2.点与圆的位置关系.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
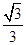 .求弦CD的长.
.求弦CD的长.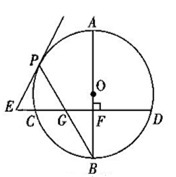
 .
.