题目内容
阅读材料:
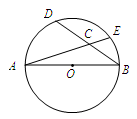
已知,如图(1),在面积为S的△ABC中, BC=a,AC="b," AB=c,内切圆O的半径为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵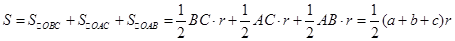 .
.
∴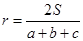 .
.
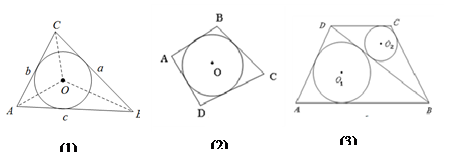
(1)类比推理:若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r;
(2)理解应用:如图(3),在等腰梯形ABCD中,AB∥DC,AB=21,CD=11,AD=13,⊙O1与⊙O2分别为△ABD与△BCD的内切圆,设它们的半径分别为r1和r2,求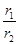 的值.
的值.
已知,如图(1),在面积为S的△ABC中, BC=a,AC="b," AB=c,内切圆O的半径为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵
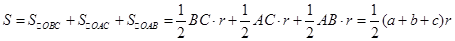 .
.∴
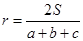 .
.
(1)类比推理:若面积为S的四边形ABCD存在内切圆(与各边都相切的圆),如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求四边形的内切圆半径r;
(2)理解应用:如图(3),在等腰梯形ABCD中,AB∥DC,AB=21,CD=11,AD=13,⊙O1与⊙O2分别为△ABD与△BCD的内切圆,设它们的半径分别为r1和r2,求
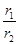 的值.
的值.(1) (2)
(2) .
.
 (2)
(2) .
.试题分析:(1)如图,连接OA、OB、OC、OD,则△AOB、△BOC、△COD和△DOA都是以点O为顶点、高都是r的三角形,根据
 即可求得四边形的内切圆半径r.
即可求得四边形的内切圆半径r.(2)过点D作DE⊥AB于点E,分别求得AE的长,进而BE 的长,然后利用勾股定理求得BD的长;然后根据
 ,
, ,两式相除,即可得到
,两式相除,即可得到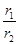 的值.
的值.试题解析:(1)如图(2),连接OA、OB、OC、OD.···················································1分
∵
 ·3分
·3分∴
 ························································································4分
························································································4分
(2)如图(3),过点D作DE⊥AB于点E,
则



 ·························································6分
·························································6分∵AB∥DC,∴
 .
.又∵
 ,
, ∴
 .即
.即 .···········································································9分
.···········································································9分

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 .求弦CD的长.
.求弦CD的长.
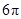 cm,那么这个的圆锥的高是
cm,那么这个的圆锥的高是
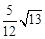 B.
B.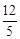 C.
C.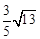 D.
D.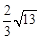
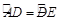 ,AB=5,BD=4,则sin∠ECB= .
,AB=5,BD=4,则sin∠ECB= .