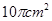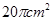题目内容
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为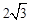 ;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=
;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=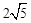 ;⑤当点D从点A运动到点B时,线段EF扫过的面积是
;⑤当点D从点A运动到点B时,线段EF扫过的面积是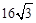 .其中正确结论的序号是 .
.其中正确结论的序号是 .

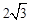 ;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=
;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=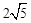 ;⑤当点D从点A运动到点B时,线段EF扫过的面积是
;⑤当点D从点A运动到点B时,线段EF扫过的面积是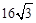 .其中正确结论的序号是 .
.其中正确结论的序号是 .
①③⑤.
试题分析:①如图,连接CD,
∵根据轴对称的性质,CE=CD,∴∠DCE=∠ECD.
又∵DF⊥DE,∴
 .∴CD="CF." ∴CE=CF. 结论①正确.
.∴CD="CF." ∴CE=CF. 结论①正确.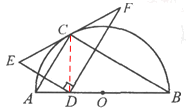
②∵由①知,EF=2CD,∴当线段EF最小时,线段CD也最小.
根据垂直线段最短的性质,当CD⊥AD时线段CD最小.
∵AB是半圆O 的直径,∴∠ACB=90°.
∵AB=8,∠CBA=30°,∴AC=4,BC=
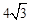 .
.当CD⊥AD时,
 ,
,∴线段EF的最小值为
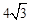 . 结论②错误.
. 结论②错误.③如图,连接CD,CO,
∵∠CAB=90°,∠CBA=30°,∴∠CAB=60°. ∴△AOB是等边三角形,∴AO=4,∠OCA=60°.
∴当AD=2时,CD⊥AD,∠OCD=∠DOA=30°.
∵根据轴对称的性质,∠EOA=∠DOA=30°,∴∠ECO=90°.
∴EF与半圆相切. 结论③正确.

④若点F恰好落在BC上,则点D,F重合于点B,AD="AB=8." 结论④错误.
⑤当点D从点A运动到点B时,线段EF扫过的面积是△ABC面积的2倍,为
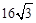 . 结论⑤正确.
. 结论⑤正确.综上所述,结论正确的是①③⑤.

练习册系列答案
相关题目
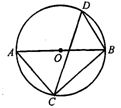
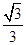 .求弦CD的长.
.求弦CD的长.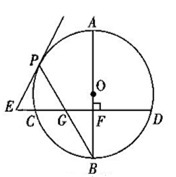

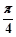 cm
cm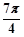 cm
cm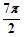 cm
cm