题目内容
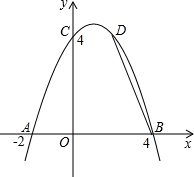
如图,抛物线y=ax2-x-
与x轴正半轴交于点A(3,0),以OA为边在x轴上方作正方形OABC,延长C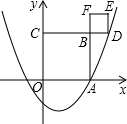 B交抛物线于点D,再以BD为边向上作正方形BDEF.
B交抛物线于点D,再以BD为边向上作正方形BDEF.
(1)求a的值;
(2)求点F的坐标.
| 3 |
| 2 |
 B交抛物线于点D,再以BD为边向上作正方形BDEF.
B交抛物线于点D,再以BD为边向上作正方形BDEF.(1)求a的值;
(2)求点F的坐标.
(1)把A(3,0)代入y=ax2-x-
中,得a=
;
(2)∵A(3,0)
∴OA=3
∵四边形OABC是正方形
∴OC=OA=3
当y=3时,
x2-x-
=3,
即x2-2x-9=0
解得x1=1+
,x2=1-
<0(舍去)
∴CD=1+
在正方形OABC中,AB=CB
同理BD=BF
∴AF=CD=1+
∴点F的坐标为(3,1+
).
| 3 |
| 2 |
| 1 |
| 2 |
(2)∵A(3,0)
∴OA=3
∵四边形OABC是正方形
∴OC=OA=3
当y=3时,
| 1 |
| 2 |
| 3 |
| 2 |
即x2-2x-9=0
解得x1=1+
| 10 |
| 10 |
∴CD=1+
| 10 |
在正方形OABC中,AB=CB
同理BD=BF
∴AF=CD=1+
| 10 |
∴点F的坐标为(3,1+
| 10 |

练习册系列答案
相关题目
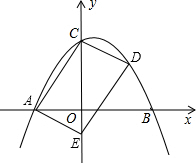
 ,动点Q以每秒2个单位长度的速度沿A→O→D→C→B运动.AO1交于轴于点E,设P、Q运动的时间为t秒.
,动点Q以每秒2个单位长度的速度沿A→O→D→C→B运动.AO1交于轴于点E,设P、Q运动的时间为t秒.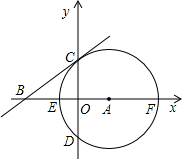 D两点,过C点作⊙A的切线BC交x轴于B.
D两点,过C点作⊙A的切线BC交x轴于B.