Question

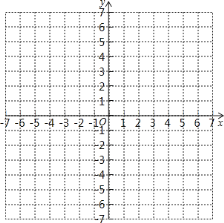
【题目】如图，在平面直角坐标系中，抛物线y＝ax2－2x+c的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，点A、B的坐标分别为(－1，0)，(3，0)，点D为抛物线的顶点，抛物线的对称轴与直线BC相交于点E.

（1）求抛物线的解析式和点C的坐标；

（2）点P是直线BC下方的抛物线上一动点，当△PBC的面积最大时，请求出P点的坐标和△PBC的最大面积；

（3）点Q是线段BD上的一动点，将△DEQ沿边EQ翻折得到△，是否存在点Q使得△与△BEQ的重叠部分图形为直角三角形？若存在，请直接写出BQ的长，若不存在，请说明理由.

Answer 1

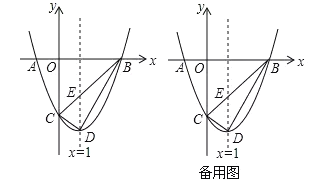
【答案】（1）y＝x2－2x－3，C(0，－3)； （2）△PBC的最大面积为， P；（3）或或.

【解析】

（1）将点A(－1，0)、B(3，0)代入抛物线解析式可求出a，c的值，得到抛物线的解析式，令x=0可求出c的坐标；

（2）直线BC解析式为：y=x-3，设与直线BC平行且在BC下方的一条直线l解析式为y=x+b，当直线l与抛物线只有一个交点时，△PBC的面积最大，联立解析式，求出当时x的值，即为P点横坐标，再根据分割面积法求出此时；

（3）根据（1）中解析式可得：D(1，-4)，直线x=1交x轴于F，BD=，然后分情况讨论，分别求出BQ的长即可.

解：（1）将点A(－1，0)、B(3，0)代入抛物线解析式y＝ax2－2x+c可得：

，解得：，

∴抛物线的解析式为y＝x2－2x－3，

当x=0时，y=-3，所以C的坐标为C（0，-3）；

（2）∵B(3，0)，C（0，-3），可得直线BC解析式为：y=x-3，

设与直线BC平行且在BC下方的一条直线l解析式为y=x+b，当直线l与抛物线只有一个交点时，△PBC的面积最大，

联立解析式，

可得，

整理得：，

∴，解得：b=，

即，解得：x=，将x=代入抛物线解析式可得，

所以P，

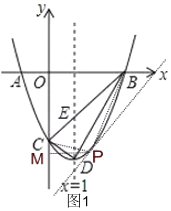
如图1，过点P作PM⊥y轴于M，∴M(0,)，

∴

∴△PBC的最大面积为

（3）根据（1）中解析式可得：D(1，-4)，直线x=1交x轴于F，BD=，

分类讨论：

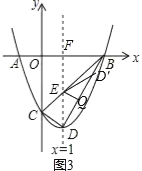
①如图3，EQ⊥DB于Q，△DEQ沿边EQ翻折得到△D’EQ，

∵∠EDQ＝∠BDF，

∴Rt△DEQ∽Rt△DBF，

∴，即，

解得DQ＝，

∴BQ＝BDDQ＝

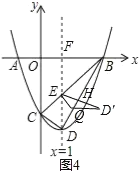
②如图4， ED′⊥BD于H，

∵∠EDH＝∠BDF，

∴Rt△DEH∽Rt△DBF，

∴，即，

解得DH＝，EH＝，

在Rt△QHD′中，设QH＝x，D′Q＝DQ＝DHHQ＝

，D′H＝D′EEH＝DEEH＝2，

∴，解得x＝1，

∴BQ＝BDDQ＝BD（DHHQ）＝BDDH＋HQ＝,；

③如图5，D′Q⊥BC于G，作EI⊥BD于I，易得EI＝，BI＝，

∵△DEQ沿边EQ翻折得到△D′EQ，

∴∠EQD＝∠EQD′，

∴EG＝EI＝，

∵BE＝，

∴BG＝BEEG＝

∵∠GBQ＝∠IBE，

∴△BQG∽△BEI，

∴，即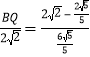

∴BQ＝

综上所述，当BQ为或或时，将△DEQ沿边EQ翻折得到△D′EQ，使得△D′EQ与△BEQ的重叠部分图形为直角三角形．