题目内容
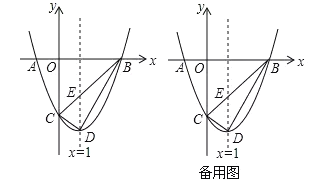
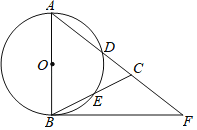
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠BAD=![]() ,求AD的长;
,求AD的长;
(3)试探究FB、FD、FA之间的关系,并证明.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() ,见解析.
,见解析.
【解析】
(1)连接AE,利用直径所对的圆周角是直角,从而判定直角三角形,利用直角三角形两锐角相等得到直角,从而证明∠ABF=90°.
(2)运用三角函数解直角三角形,并用勾股定理求出AD.
(3)利用已知条件证得△ABF∽△BDF,就可以得出三条线段F![]() 之间的关系.
之间的关系.
解:(1)证明:连结![]() .
.
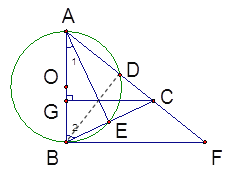
∵![]() 是
是![]() 的直径
的直径
∴![]()
∴![]()
∵![]() ∴
∴![]()
∵![]() ∴
∴![]()
∴![]() ,即
,即![]()
∴![]()
∴直线![]() 是
是![]() 的切线.
的切线.
(2)连接![]() ,则
,则![]() 为直角三角形.
为直角三角形.
∴![]() ∴
∴![]()
由勾股定理可得![]() ;
;
(3)![]()
证明:∵![]()
∴![]()
∴![]()
∴![]()

 学练快车道口算心算速算天天练系列答案
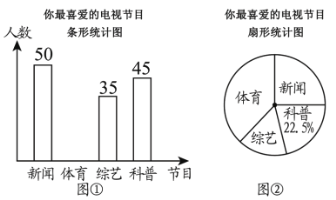
学练快车道口算心算速算天天练系列答案【题目】为了解八年级500名学生的身体素质情况,体育老师从中随机抽取50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出如下频数分布表和频数分布直方图(不完整):
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 |
|
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
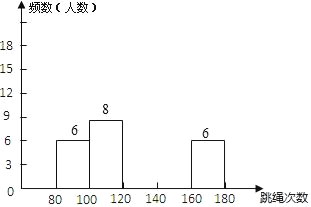
完成下列问题:
(1)请把上面的频数分布表和频数分布直方图补充完整;
(2)这个样本数据的中位数落在第 组;次数在140≤x<160这组的频率为 ;
(3)若八年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120合格,试问该年级合格的学生有多少人?
【题目】小明和小丽暑期参加工厂社会实践活动,师傅将他们工作第一周每天生产的合格产品的个数整理成如表两组数据,那么关于他们工作第一周每天生产的合格产品个数,下列说法中正确的是( )
小明 | 2 | 6 | 7 | 7 | 8 |
小丽 | 2 | 3 | 4 | 8 | 8 |
A. 小明的平均数小于小丽的平均数
B. 两人的中位数相同
C. 两人的众数相同
D. 小明的方差小于小丽的方差