Question

【题目】在△ABC中.BC边的长为x,BC边上的高为y,△ABC的面积为2．

(1)y关于x的函数关系式是________， x的取值范围是________；

(2)在平面直角坐标系中画出该函数图象；

(3)将直线y=-x+3向上平移a(a>0)个单位长度后与上述函数图象有且只有一个交点，请求出此时a的值．

Answer 1

【答案】（1）y=，x＞0；（2）见解析；（3）1

【解析】

（1）根据三角形的面积公式即可得出函数关系式，再根据实际意义得出x的取值范围；

（2）在平面直角坐标系中画出图像即可；

（3）得到平移后的一次函数表达式，再和反比例函数联立，得到一元二次方程，再结合交点个数得到根的判别式为零，即可求出a值.

解：（1）由题意可得：

S△ABC=xy=2，

则：y=，

其中x的取值范围是x＞0，

故答案为：y=，x＞0；

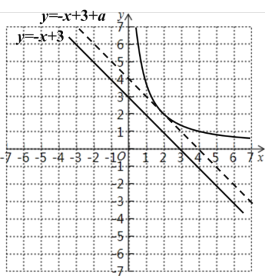
（2）函数y=（x＞0）的图像如图所示；

（3）将直线y=-x+3向上平移a(a>0)个单位长度后得到y=-x+3+a，

若与函数y=（x＞0）只有一个交点，

联立：，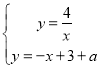

得：，

则，

解得：a=1或-7（舍），

∴a的值为1.