Question

【题目】如图，将一个正方形纸片OABC放置在平面直角坐标系中，其中A（1，0），C（0，1），P为AB边上一个动点，折叠该纸片，使O点与P点重合，折痕l与OP交于点M，与 对角线AC交于Q点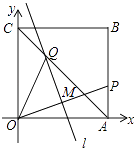

（Ⅰ）若点P的坐标为（1， ），求点M的坐标；
（Ⅱ）若点P的坐标为（1，t）
①求点M的坐标（用含t的式子表示）（直接写出答案）
②求点Q的坐标（用含t的式子表示）（直接写出答案）
（Ⅲ）当点P在边AB上移动时，∠QOP的度数是否发生变化？如果你认为不发生变化，写出它的角度的大小．并说明理由；如果你认为发生变化，也说明理由．

Answer 1

【答案】解：（Ⅰ）过M作ME⊥x轴于点E，如图1，

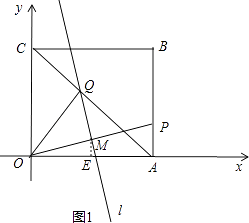
由题意可知M为OP中点，

∴E为OA中点，

∴OE= OA= ，ME= AP= ，

∴M点坐标为（ ， ）；

（Ⅱ）①同（Ⅰ），当P（1，t）时，可得M（ ， t）；

②过Q点作QD⊥OA于D，作QE⊥AB与E，连接QP．

∵Q点在AC上，

∴QD=AD=AE=QE，

在Rt△OQD和Rt△OPE中，

∴Rt△OQD≌Rt△OPE，

∴OD=PE，

设OD=PE=x，则AD=1﹣x，AE=t+x，则1﹣x=t+x，解得x= ，

QD=AE=t+x= ．

∴Q点坐标为（ ， ）．

（Ⅲ）不变化，∠QOP=45°．

理由如下：由（Ⅱ）②可知Q点坐标为（ ， ），

根据勾股定理得，

OQ2=OD2+QD2=（ ）2+（ ）2= ，

QP=OQ，

OP2=OA2+AP2=1+t2，

∴OQ2+QP2=OP2，

∴△OPQ是以OP为斜边的等腰直角三角形，

∴∠QOP=45°，

即∠QOP不变化．

【解析】（Ⅰ）由题意可知M为OP中点，得到E为OA中点，得到M点坐标为（ ， ）；（Ⅱ）①同（Ⅰ），当P（1，t）时，可得M（ ，t）；②由题意得到QD=AD=AE=QE，Rt△OQD≌Rt△OPE，OD=PE，得到Q点坐标为（ ， ）；（Ⅲ）由（Ⅱ）②可知Q点坐标，根据勾股定理得到OQ2+QP2=OP2，所以△OPQ是以OP为斜边的等腰直角三角形，∠QOP不变化；此题是综合题，难度较大，计算和解方程时需认真仔细.
【考点精析】解答此题的关键在于理解翻折变换（折叠问题）的相关知识，掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．