Question

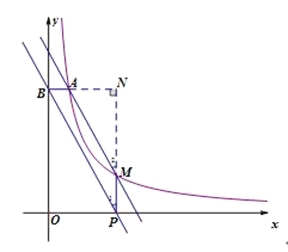
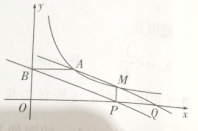
【题目】如图，点A(3,2)和点M(m,n)都在反比例函数y=(x>0)的图像上，

(1)求k的值,并求当m=4时，直线AM的解析式;

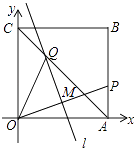
(2)过点M作MP⊥x轴,垂足为P，过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形;

(3)在(2)的条件下，四边形ABPQ能否为菱形?若能,请求出m的值;若不是,请说明理由.

Answer 1

【答案】（1）k=6，直线AM的解析式为；（2）详见解析；（3）能，当时，四边形ABPQ是菱形．

【解析】

试题（1）将A坐标代入反比例解析式求出k的值即可；由k的值可得反比例解析式，将m=4代入反比例解析式求出n的值，从而确定M坐标，由待定系数法即可求出直线AM解析式；（2）如图，延长BA、PM相交于N．则∠N=90°，由A（3,2），M（m，n）可得B（0,2），P（m，0），N（m，2）．又因点M（m，n）都在反比例函数的图像上，所以，利用三角函数可得，，所以，即∠1=∠2，根据同位角相等两直线平行即可得AM∥BP，再由AB∥PQ即可判定四边形ABPQ是平行四边形；（3）当四边形ABPQ是菱形时，PB=AB=3，在直角三角形BOP中，由勾股定理可列方程，解得m的值即可．

试题解析：（1）点A（3,2）在反比例函数的图像上

所以

当m=4时，则n=，所以M（4，）

设直线AM的解析式为

则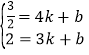

解得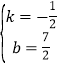

所以直线AM的解析式为

（2）延长BA、PM相交于N．则∠N=90°

∵A（3,2），M（m，n）

∴B（0,2），P（m，0），N（m，2）

∴BN=m，PN=2，AN=m-3，MN=2-n

∴

∴

∴∠1=∠2

∴AM∥BP

∵AB∥PQ

∴四边形ABPQ是平行四边形

（3）能．当四边形ABPQ是菱形时，PB=AB=3,在直角三角形BOP中，∵

∴

∴

∴当时，四边形ABPQ是菱形．