题目内容
【题目】如图,在△ABC中,AC=BC,以BC边为直径作⊙O交AB边于点D,过点D作DE⊥AC于点E.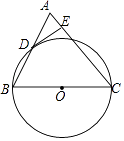
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径等于 ![]() ,cosB=
,cosB= ![]() ,求线段DE的长.
,求线段DE的长.
【答案】
(1)解:证明:连结OD.
∵AC=BC,
∴∠A=∠B,
∵OB=OD,
∴∠B=∠ODB,
∴∠A=∠ODB,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线,
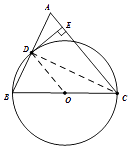
(2)解:如图,连结CD.

∵⊙O的半径等于 ![]() ,
,
∴BC=3,∠CDB=90°,
在Rt△CDB中,
cosB= ![]() =
= ![]() ,
,
∴BD=1, ![]() ,
,
∵AC=BC=3,∠CDB=90°.
∴AD=BD=1,
解法一:在Rt△ADC中, ![]() ,
,
解法二:∵∠A=∠A,∠ADC=∠AED=90°,
∴△ACD∽△ADE.
∴ ![]() .
.
∴ ![]()
【解析】(1)根据等腰三角形的性质,等边对等角,得到角相等,得出平行线,得出DE是⊙O的切线;(2)根据在Rt△CDB中,由三角函数和勾股定理求出AC=BC、CD、AD=BD的值,由角相等得出△ACD∽△ADE,得到比例,求出DE的值.
【考点精析】通过灵活运用等腰三角形的性质和解直角三角形,掌握等腰三角形的两个底角相等(简称:等边对等角);解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:
七年级(3)班学生到图书馆的次数统计表
到图书馆的 | 0次 | 1次 | 2次 | 3次 | 4次及 |
人数 | 5 | 10 | m | 8 | 12 |
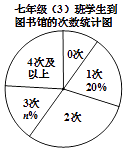
(1)求图表中m,n的值;
(2)该年级学生共有300人,估计这周到图书馆的次数为“4次及以上”的学生大约有多少人?