题目内容
【题目】在平面直角坐标系![]() 中,
中,![]() 如图所示,点
如图所示,点![]() .
.
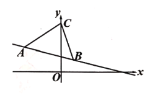
(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积;
的面积;
(3)一次函数![]() (
(![]() 为常数).
为常数).
①求证:一次函数![]() 的图象一定经过点
的图象一定经过点![]() ;
;
②若一次函数![]() 的图象与线段
的图象与线段![]() 有交点,直接写出
有交点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)①见解析,②
;(3)①见解析,②![]() 且
且![]() .
.
【解析】
(1)根据待定系数求解析式即可;
(2)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 点,求出点D的坐标,然后根据
点,求出点D的坐标,然后根据![]() 可得出结果;
可得出结果;
(3)①把一次函数![]() 整理为
整理为![]() 的形式,再令x+3=0,求出y的值即可;
的形式,再令x+3=0,求出y的值即可;
②根据直线![]() 一定经过点A,而且与线段BC有交点,可得直线
一定经过点A,而且与线段BC有交点,可得直线![]() 在绕着点A从直线AC顺时针旋转到直线BC之间的区域,再结合a≠0从而得出结果.
在绕着点A从直线AC顺时针旋转到直线BC之间的区域,再结合a≠0从而得出结果.
解:(1)设直线![]() 的解析式是
的解析式是![]() ,将点
,将点![]() ,点
,点![]() 代入的,得
代入的,得
![]() ,解得,
,解得,
∴直线![]() 的解析式是
的解析式是![]() ;
;
(2)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 点,
点,
则点![]() 的坐标为
的坐标为![]() ,
,
![]() ;
;
(3)①证明:∵![]() ,
,
令x+3=0,得x=-3,此时y=2.
∴![]() 必过点
必过点![]() ,即必过
,即必过![]() 点;
点;
②当直线![]() 与直线AC重合时,可得4=3a+2,解得a=
与直线AC重合时,可得4=3a+2,解得a=![]() ,
,
当直线![]() 与直线AB重合时,可得1=a+3a+2,解得a=
与直线AB重合时,可得1=a+3a+2,解得a=![]() ,
,
∴a的取值范围是:![]() 且
且![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目