题目内容
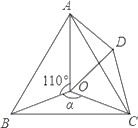
【题目】如图,在正方形ABCD中,点E为AB的中点,F为线段BE上任意一点,将线段EF绕点E逆时针旋转90°,得到线段EG.

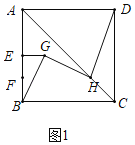
(1)按请按要求补全图形:连接BG过点G作GH⊥BG,交对角线AC于点H,连接DH;
(2)判断DH与GH的数量关系并加以证明.
【答案】(1)见解析;(2)结论:DH=![]() GH.理由见解析.
GH.理由见解析.
【解析】
(1)根据要求画出图形即可.
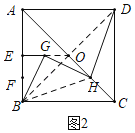
(2)结论:DH=![]() GH.如图2中,连接BD交AC于O,连接BH,OG.想办法证明△BGH是等腰直角三角形,DH=BH即可解决问题.
GH.如图2中,连接BD交AC于O,连接BH,OG.想办法证明△BGH是等腰直角三角形,DH=BH即可解决问题.
(1)如图1所示:
(2)结论:DH=![]() GH.
GH.
理由:如图2中,连接BD交AC于O,连接BH,OG.
∵AE=EB,GE⊥AB,
∴GE是AB的垂直平分线,
∴点E,G,O共线,
∵AE=EB,AO=OC,
∴EO∥BC,
∴∠EOB=∠OBC=45°,
∵四边形ABCD是正方形,
∴∠BOH=∠BGH=90°,
∴B,G,O,H四点共圆,
∴∠GOB=∠GHB=45°,
∴△BGH是等腰直角三角形,
∴BH=![]() GH,
GH,
在△AHB和△AHD中,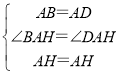
∴△AHB≌△AHD(SAS),
∴DH=BH,
∴DH=![]() GH.
GH.

练习册系列答案
相关题目