题目内容
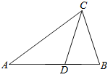
【题目】如图，等腰
的顶角
的度数是
，点
是腰
的黄金分割点
，将
绕着点
按照顺时针方向旋转一个角度后点落在点
处，联结
，当
时，这个旋转角是________度．
【答案】
或
【解析】
先证出点D是腰AB的黄金分割点时，CD是∠ACB的平分线，当AE∥CD时，分两种情况，利用图形解出旋转角为72°或108°．
假设CD为∠ACB的平分线，
∵∠A=36°，
∴∠B=∠ACB=72°，
∴∠ACD=∠DCB=36°，
∴BC=DC=AD，
∴△CDB∽△ABC，
∴
，
∴AD：AB=DB：AD，
点D是腰AB的黄金分割点，
∴CD是∠ACB的平分线，
（1）如图1，
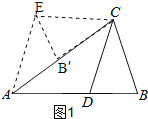
∵AE∥CD时，
∴∠EAC=∠ACD=36°，
∴EC∥AD，
∵AD=CD
∴四边形ADCE是菱形．
∴此时这个旋转角72°；
（2）如图2，
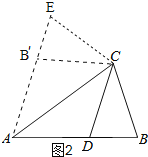
∵AE∥CD时，
∴∠EAC=∠ACD=36°，
∴B′C∥AD，
∵AD=CD
∴四边形ADCB′是菱形．
∴∠B′CD=72°，
∴∠EB′C=72°，∠B′EC=72°，
∴此时这个旋转角36°+36°+36°=108°，
故答案为：72或108．
【题目】学校在八年级新生中举行了全员参加的数学应用能力大赛，试卷题目共10题，每题10分.现分别从三个班中各随机取10名同学的成绩（单位：分），收集数据如下：
1班：90，70，80，80，80，80，80，90，80，100；
2班：70，80，80，80，60，90，90，90，100，90；
3班：90，60，70，80，80，80，80，90，100，100.
整理数据：
人数 班级 | 60分人数 | 70分人数 | 80分人数 | 90分人数 | 100分人数 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
平均数 | 中位数 | 众数 | |
83 | 80 | 80 | |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
分析数据：
根据以上信息回答下列问题：
（1）请直接写出表格中
，
，
，
的值；
（2）比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好？请说明理由（写两条支持你结论的理由）.
