题目内容
己知一次函数与反比例函数图象都经过A(-2,-1)、B(n,2)两点.
(1)求这两个函数的解析式;
(2)求三角形AOB的面积S△AOB.

(1)求这两个函数的解析式;
(2)求三角形AOB的面积S△AOB.

(1)设反比例函数解析式为y=
(k≠0),
由一次函数与反比例函数都经过A(-2,-1),
故将x=-2,y=-1代入反比例解析式得:-1=
,
解得:k=2,
∴反比例函数解析式为y=
;
又B(n,2)在反比例函数图象上,
∴将x=n,y=2代入反比例函数解析式得:2=
,
解得:n=1,即B(1,2),
设一次函数解析式为y=px+q(p≠0),
将A和B的坐标代入得:
,
解得:
,
∴一次函数解析式为y=x+1;
(2)设一次函数与x轴交于C点,过A作AD⊥x轴于D点,过B作BE⊥x轴于E点,如图所示:
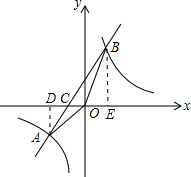
对应一次函数y=x+1,令y=0,解得:x=-1,故C(-1,0),即OC=1,
又A(-2,-1),B(1,2),
∴AD=1,BE=2,
则S△OAB=S△AOC+S△BOC=
OC•AD+
OC•BE=
+1=
.
| k |
| x |
由一次函数与反比例函数都经过A(-2,-1),
故将x=-2,y=-1代入反比例解析式得:-1=
| k |
| -2 |
解得:k=2,
∴反比例函数解析式为y=
| 2 |
| x |
又B(n,2)在反比例函数图象上,
∴将x=n,y=2代入反比例函数解析式得:2=
| 2 |
| n |
解得:n=1,即B(1,2),
设一次函数解析式为y=px+q(p≠0),
将A和B的坐标代入得:
|
解得:
|
∴一次函数解析式为y=x+1;
(2)设一次函数与x轴交于C点,过A作AD⊥x轴于D点,过B作BE⊥x轴于E点,如图所示:

对应一次函数y=x+1,令y=0,解得:x=-1,故C(-1,0),即OC=1,
又A(-2,-1),B(1,2),
∴AD=1,BE=2,
则S△OAB=S△AOC+S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目












