题目内容
【题目】在△ABC中,∠B=45°, AM⊥BC,垂足为M.
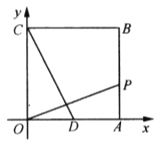
(1)如图1,若AB=4![]() ,BC=7,求AC的长;
,BC=7,求AC的长;
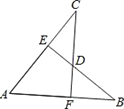
(2)如图2, 点D是线段AM上一点,MD=MC,点E是△ABC外一点,CE=CA,连接ED并延长交BC于点F,且∠BDF=∠CEF,
求证①AC=BD;
②BF=CF.

【答案】(1)5;(2)见解析.
【解析】
(1)先由AM=BM=ABcos45°=4可得CM=3,再由勾股定理可得AC的长;
(2)①由AM⊥BC,得∠AMC=∠BMD=90°,再由三角形全等可证AC=BD;
②延长EF到点G,作BG∥EC,可得∠G=∠CEF,证得BG=CE,再证△BFG≌△CFE可得BF=CF.
(1)解:∵AM⊥BC,
∴∠AMB=90°.
∵∠B=45°,
∴∠BAM=90°-45°=45°.
∴BM=AM.
∵AB=![]() ,
,
∴BM=4.
∴CM=BC-BM=3.
∵∠AMC=90°,
∴AC=![]() .
.
(2)①∵AM⊥BC,
∴∠AMC=∠BMD=90°.
∵MC=MD,AM=BM,
∴△AMC≌△BMD.
∴AC=BD.
②延长EF,过B作BG∥EC交EF延长线于点G.
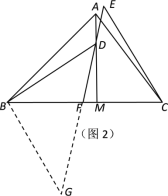
∵BG∥CE,
∴∠G=∠CEF.
∵∠BDF=∠CEF,
∴∠G=∠BDF.
∴BG=BD.
∵AC=CE,AC=BD,
∴BG=CE.
∵∠BFG=∠CFE,
∴△BGF≌△CEF.
∴BF=CF.

 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案【题目】一组对边平行,另一组对边相等且不平行的四边形叫做等腰梯形.
(1)类比研究
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对四边形进行研究,完成表.
四边形 | 对称性 | 边 | 角 | 对角线 |
平行 | . | 两组对边分别平行,两组对边分别相等. | 两组对角 | 对角线互相平分. |
等腰 | 轴对称图形,过平行的一组对边中点的直线是它的对称轴. | 一组对边平行,另一组对边相等. | . | . |
(2)演绎论证
证明等腰梯形有关角和对角线的性质.
已知:在等腰梯形ABCD中,AD∥BC,AB=DC,AC、BD是对角线.
求证:
证明:
揭示关系
我们可以用图来揭示三角形和一些特殊三角形之间的关系.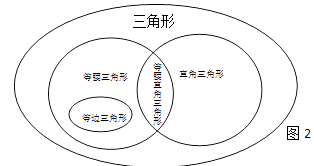
(3)请用类似的方法揭示四边形、对角线相等的四边形、平行四边形、矩形以及等腰梯形之间的关系.