题目内容
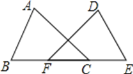
【题目】如图,在ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF. 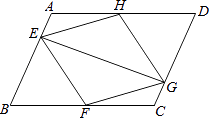
(1)求证:△AEH≌△CGF;
(2)求证:四边形EFGH是菱形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C.
∴在△AEH与△CGF中,  ,
,
∴△AEH≌△CGF(SAS)
(2)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠B=∠D.
∵AE=CG,AH=CF,
∴EB=DG,HD=BF.
∴△BEF≌△DGH.
∴EF=HG.
又∵△AEH≌△CGF,
∴EH=GF.
∴四边形HEFG为平行四边形.
∴EH∥FG,
∴∠HEG=∠FGE.
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠FGE=∠FEG,
∴EF=GF,
∴四边形EFGH是菱形
【解析】(1)根据全等三角形的判定定理SAS证得结论;(2)欲证明四边形EFGH是菱形,只需推知四边形EFGH是平行四边形,然后证得该平行四边形的邻边相等即可.
【考点精析】掌握平行四边形的性质和菱形的判定方法是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

【题目】某农产品生产基地收获红薯192吨,准备运给甲、乙两地的承包商进行包销.该基地用大、小两种货车共18辆恰好能一次性运完这批红薯,已知这两种货车的载重量分别为14吨/吨和8吨/辆,运往甲、乙两地的运费如下表:
车型 | 运费 | |
运往甲地/(元/辆) | 运往乙地/(元/辆) | |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
(1)求这两种货车各用多少辆;
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,总运费为w元,求w关于a的函数关系式;
(2)在(2)的条件下,若甲地的承包商包销的红薯不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费.
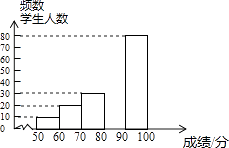
【题目】中华文明,源远流长:中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 20 | 0.10 |
70≤x<80 | 30 | b |
80≤x<90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b=;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?