题目内容
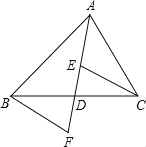
【题目】如图(1),是两个全等的直角三角形(直角边分别为a,b,斜边为c).
(1)用这样的两个三角形构造成如图(2)的图形(B,E,C三点在一条直线上),利用这个图形,求证:a2+b2=c2
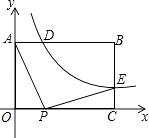
(2)当a=1,b=2时,将其中一个直角三角形放入平面直角坐标系中(如图(3)),使直角顶点与原点重合,两直角边a,b分别与x轴、y轴重合.
请在坐标轴上找一点C,使△ABC为等腰三角形.
写出一个满足条件的在x轴上的点的坐标: ;
写出一个满足条件的在y轴上的点的坐标: ,这样的点有 个.

【答案】(1)详见解析;(2)(﹣1,0);(0,2+![]() ),4.
),4.
【解析】
(1)由图知,梯形的面积等于三个直角三角形的面积之和,用字母表示出来,化简后,即证明勾股定理;
(2)根据等腰三角形的性质分三种情况讨论即可求解.
(1)由图可得,![]() ×(a+b)(a+b)=
×(a+b)(a+b)=![]() ab+
ab+![]() c2+
c2+![]() ab,
ab,
整理得![]() =
=![]() ,
,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
(2)一个满足条件的在x轴上的点的坐标:(﹣1,0);
一个满足条件的在y轴上的点的坐标:(0,2+![]() ),这样的点有 4个.
),这样的点有 4个.
故答案为:(﹣1,0);(0,2+![]() ),4.
),4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目